The conference took place from Monday July 15th to Friday July 19th. The programme consisted of three days of invited review (45 minutes + 15 minutes for questions) and contributed talks (20 minutes + 5 minutes for questions), followed by two days of open discussion sessions. A detailed breakdown of the schedule is provided in the following table, with abstracts, titles and slides from all talks further below.

	Monday	Tuesday	Wednesday	Thursday	Friday
08.30	Bus pickup at Burlington hotel
09.00	Niels WarburtonOrbital evolution with the self-force: progress and challenges	Sam DolanApproaches to self-force calculations on Kerr	Barak KolEffective field theory approach to post-Newtonian self-force	Bus pickup at 9AM9.30-10.30Kerr & gaugeLeor Barack	Bus pickup at 9AMMeeting space available for open discussions
10.00	Jonathan GairProspects for extreme-mass-ratio inspiral detection	Adam PoundSecond-order self-force: results and prospects	Abraham HarteSelf-interaction and extended bodies
11.00	Break	Break	Break	11.00-12.00Orbital evolutionPeter Diener
11.30	Patxi RitterMaarten van de MeentDiscussion	Barry WardellPeter DienerJonathan Thornburg	Marc CasalsBrien NolanShahar Hadar
12.45	Lunch	Lunch	Lunch	Lunch
14.15	Takahiro TanakaSoichiro IsoyamaBarak Kol	Seth HopperErik ForsethThomas Osburn	Peter ZimmermanAbhay ShahPriscilla CañizaresBernard Whiting	14.00-15.00Second orderAdam Pound
15.30	Break	Break		15.30-16.30Functional methodsBernard Whiting
16.00	Chad GalleyDmitri Gal'tsovDiscussion	Anna HeffernanPatrick NolanCesar Merlin	Excursion to Howth including dinner at Aqua restaurant		Bus returning to Burlington hotel departs at 4PM
17.30	Bus returning to Burlington hotel	Bus returning to Burlington hotel		Bus returning to Burlington hotel

Invited review talks

Abraham Harte [Slides]
Self-interaction and extended bodies
This talk will review the theory of motion associated with extended objects. Non-perturbative notions of momentum and center of mass will be discussed as well as the effects of self-interaction on the evolution of these quantities. Some new ideas regarding the use of geometric flows will also be mentioned. These are operations intended to smoothly deform the metric while simultaneously preserving all forces and torques. Regular fields/metrics used for the self-force are related to physical fields via flows of this type.

Adam Pound [Slides]
Second-order self-force: results and prospects
Modeling binary inspirals has been a primary impetus for the self-force program. However, self-force results have mostly been confined to first-order corrections to a test-particle description, while an accurate model of an inspiral must incorporate second-order effects. This requires two analytical ingredients: a concrete method of solving the second-order Einstein equation for the field generated by a small object; and an expression for the force that the field exerts back on the object. I describe recent results for these ingredients and the relation between the formalisms used to derive them. With the ingredients at hand, concrete numerical calculations of second-order self-force effects should soon be realized, and I discuss progress toward that goal.

Barak Kol [Slides]
Effective field theory approach to post-Newtonian self-force
We formulate an effective field theory (EFT) which describes the post-Newtonian (PN) inspiral of two gravitating bodies including dissipative effects, thus formulating the computation to all orders.

Jonathan Gair [Slides]
Prospects for extreme-mass-ratio inspiral detection
The detection of gravitational waves from extreme-mass-ratio inspirals (EMRIs) will require a detector operating in the milihertz frequency band, which is only accessible from space. The withdrawal of NASA funding from the LISA project prompted a redesign as an ESA -only mission NGO. However, NGO was not selected for the L1 mission launch opportunity. ESA is now undergoing a theme selection for the L2/L3 launch opportunities in 2028 and 2034. I will describe this ongoing process and discuss the potential of an L2 LISA-like mission for the detection and characterisation of EMRIs.

Niels Warburton [Slides]
Orbital evolution with the self-force: progress and challenges
In this talk I review the progress of self-force calculations concentrating on the challenges presented in using self-force results to compute inspirals. In particular I will discuss orbit evolution within the 'osculating orbits with the geodesic self-force' approximation. There are ongoing efforts to quantify the phase error from using this approximation and I will present some preliminary results in this direction.

Sam Dolan [Slides]
Approaches to self-force calculations on Kerr

Contributed talks

Abhay Shah [Slides]
Extraction of very high precision post-Newtonian parameters from self-force computations
We report progress in extracting high-precision conservative & dissipative pN parameters (linear in mass-ratio) for a particle in circular orbits about a Schwarzschild blackhole from the self-force computations in a modified radiation gauge and RWZ gauge. Apart from integral pN coefficients, this comparison discovered half-integral, conservative pN coefficients whose presence were later confirmed by the pN theory. Because of the extraordinarily high precision, we can extract analytical values of higher order pN coefficients. With the help of recent work by Fujita, we also extract pN coefficients for the ingoing flux at the event horizon. This work is an extension of the earlier work by Blanchet et al. We will conclude the talk by reporting our progress on extracting spin-dependent pN coefficients for circular orbits in Kerr spacetime.

Anna Heffernan, Adrian Ottewill and Barry Wardell [Slides]
Regularization of the self-force: applications to Kerr spacetime and accelerated motion
Using the regularisation techniques presented at last year's Capra, we have advanced our calculations in two directions; equatorial eccentric orbits in Kerr space-time and accelerated motion in Schwarzschild space-time. We present the applications of these results and their implications.

Barak Kol [Slides]
Self-force from equivalent periodic sources

Barry Wardell, Niels Warburton [Slides]
Effective source self-force calculations in the frequency domain
The calculation of the self-force is commonly approached using either mode-sum regularization or effective source techniques; up to now these have been considered as two distinct computational methods. In this talk, we apply the effective source approach in the frequency domain and demonstrate how the standard mode-sum regularization scheme may recovered as a specific limit. In the process, we also show the mathematical equivalence of window-function and world-tube effective source schemes. To demonstrate our approach, we initially work with a scalar toy model which captures most of the essential features without unnecessary complexity. We then apply the same techniques to the first-order-in-the-mass-ratio gravitational self-force problem and, as an aside, derive for the first time the regularization parameters for the individual tensor harmonic components of the metric perturbation.

Bernard Whiting [Slides]
Reflections on evolving Capra

Brien Nolan, Marc Casals [Slides]
Singularity structure of the retarded Green function in Schwarzschild spacetime from large- 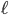$\ell$ asymptotics
The fourfold singularity structure of the retarded Green function 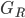$G_R$ for wave equations in curved spacetimes with caustics has been discussed on several occasions in the recent literature in the context of the self-force problem. We provide further detail on this fourfold structure for waves on Schwarzschild black holes by application of large 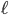$\ell$ asymptotic anaylsis of the 1+1 dimensional Regge-Wheeler equation and resummation of the asymptotic solution for the 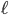$\ell$ -modes. This allows us to relate the leading order coefficients of the global singular structure of 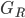$G_R$ to coefficients of the local singular structure (i.e., the Hadamard form). We also discuss the feasability of using this approach to the calculation of 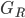$G_R$ in the self-force problem.

Cesar Merlin [Slides]
Gravitational self-force from curvature scalars in a locally-deformed radiation gauge
Calculations of the gravitational self-force (GSF) on a point mass in curved spacetime require as input the metric perturbation in a gauge that is sufficiently regular at the particle's location, such as the Lorenz gauge. A basic challenge in the program to compute the GSF for orbits around a Kerr black hole is that the standard procedure for reconstructing the metric perturbation in Kerr spacetime is formulated in a "radiation" gauge, which is not sufficiently regular. Here we describe a new practical scheme for the GSF is Kerr spacetime, addressing this issue. The GSF is formulated in a suitable regular gauge, constructed through a certain local gauge deformation of a radiation-gauge perturbation. We derive a practical mode-sum formula for the GSF in this gauge, which is analogous to the standard Lorenz-gauge formula but uses as input the multiple modes of a radiation-gauge perturbation, with corresponding corrections to the values of the regularization parameters. 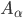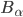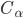We obtain these corrections analytically, and find that the parameters usually denoted $A_{\alpha}$ , $B_{\alpha}$ and $C_{\alpha}$ retain their Lorenz-gauge values, while, in general, 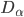$D_{\alpha}$ is modified. We explain how the nonzero correction we find for 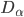$D_{\alpha}$ arises directly as a consequence of the violation of Gralla's invariance criteria. We discuss the relation to a closely related approach by Shah et. We present preliminary numerical results for the GSF including the correction for 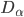$D_{\alpha}$ for circular orbits around a Schwarzschild black hole and agreement for the gauge invariant quantity $H$ .

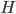Chad Galley [Slides]
Gravitational self-force in the ultra-relativistic regime
Using the effective field theory formalism, I discuss the gravitational self-force on a small compact object in the ultra-relativistic regime where the boost factor 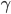$\gamma$ may become arbitrarily large. Drawing parallels with the large N limit in quantum field theory, a parameter 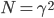$N = \gamma^2$ is introduced and used to show how the effective action admits a well defined expansion in the ultra-relativistic limit. In this limit, many simplifications arise allowing one to compute self-force effects to high orders in perturbation theory. In particular, diagrams with nonlinear bulk interactions are subleading so that only diagrams with nonlinearities in the worldline couplings, which are significantly easier to compute, survive in the large N/ultra-relativistic limit. Results are presented for the self-force through fourth order and then specialized to circular orbits in a Schwarzschild background where expressions greatly simplify. Finally, I discuss interesting aspects of the problem of finding the self-force in the exact massless limit for a "photon" moving in a black hole spacetime. 

Dmitry Gal'tsov [Slides]
Gravitational radiation reaction at ultrahigh energies
As was shown in 1974 by Penrose in general relativity and more recently generalized to TeV-scale gravity models with large extra dimensions, a black hole is created in ultra-high energy collisions of elementary particles with impact parameters satisfying Thorne's hoop conjecture. Dvali et al. suggested that this essentially classical effect may cure perturbative non-unitarity of quantum gavity by "classicalization", since distances smaller than the gravitational radius of the black hole can not be probed in such collisions. There remains the problem of impact parameters beyond the hoop inequality, in which case the balck hole is not created. We argue that in this region classical gravitational radiation damping might play similar role. At transplanckian energies gravity not only becomes the dominant force but also is well described by classical theory. Computation of classical gravitational bremsstrahlung in transplanckian collisions and gravitational synchrotron radiation shows that the energy loss increases dramatically with the number of extra dimensions implying that quantum effects are damped by classical radiation. This may be regarded as a second classicalization mechanism in multidimensional quantum gravity in addition the to black hole creation.

Erik Forseth [Slides]
Direct Integration of the Lorenz Gauge Equations in the Frequency Domain: Unconstrained Approach to the EHS Method
We outline how the method of extended homogeneous solutions (EHS) is applied to a system of equations to directly integrate the Lorenz gauge field equations for eccentric orbits on a Schwarzschild background. We then discuss some of the issues encountered when working with the unconstrained equations in Lorenz gauge. The method uses homogeneous solutions to the field equations that do not, on their own, satisfy the Lorenz gauge condition. Nevertheless, integration through the source region constrains the particular solution such that the gauge condition is then satisfied. We also examine the difficulties with integrating near-static modes, and discuss a quad-precision code that was built to handle these cases and maintained desired accuracy.

Jonathan Thornburg, Barry Wardell [Slides]
Scalar self-force for highly eccentric orbits in Kerr spacetime
The Barack-Golbourn-Vega-Detweiler effective source regularization provides a general method for computing radiation-reaction effects in Kerr spacetime. Here we describe the application of this technique (combined with an m-mode Fourier decomposition and a worldtube scheme) to compute the scalar self-force on a particle on a highly eccentric (bound, geodesic) orbit in Kerr spacetime, accurate to 1st order in the mass ratio.

Maarten van de Meent [Slides]
Resonances in orbital dynamics
Bound geodesic motion in a Kerr spacetime is an integrable system. As such the dynamics can be described by a trivial set of trivial equations of motions involving three constant frequencies and three linearly growing angles. When considering the correction to these equations of motion due to gravitational self-force in EMRIs, we can generically restrict our attention to the secular contributions, because the oscillatory part (which has a much shorter time scale than the inspiral time scale). This picture changes when the system passes through a situation where the frequencies have an (low) integer ratio. In that situation some of the oscillatory correction temporarily become (effectively) constant producing a significant correction to the orbit (and the emitted waveform). In this talk I will review some of the recent work done to quantify these effects, particularly focusing on the (im)possibility of sustained resonances.

Marc Casals [Slides]
Self-force in Schwarzschild space-time via the method of matched expansions
We present a calculation of the self-force using the method of matched expansions for the case of a scalar charge in Schwarzschild spacetime. The self-force may be calculated by integrating the Green function for the wave equation over the past world line of the small object. The method of matched expansions is a semi-analytic method which consists of splitting this integral into two different time regimes. Inside a local neighbourhood of the charge, this method uses the Hadamard form for the Green function in order to render regularization trivial. Outside this local neighbourhood, we calculate the Green function using a spectral decomposition into poles (quasinormal modes) and a branch cut integral in the complex-frequency plane. This method offers an insight into the origin of the self-force.

Patrick Nolan [Slides]
Electromagnetic and gravitational self-force calculations in Schwarzschild spacetime
We discuss the mode-sum method for calculating the self-force for an electromagnetic and a massive particle in a circular orbit around a Schwarzschild black hole. The self-force is regularised by subtracting recently obtained 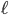$\ell$ -mode parameters to produce highly accurate results.

Patxi Ritter, Alessandro Spallicci [Slides]
I. Numerical method for generic orbits. II. Radial fall evolution
For the Regge-Wheeler and Zerilli wave equations, a time domain method, based upon the jump conditions, was applied to radial fall at first order (Phys. Rev. D 83, 064029, 2011), and later at fourth order (Class. Q. Grav. 28, 134012, 2011). We have also successfully applied it to generic orbits of EMRI (Extreme Mass Ratio Inspiral) sources. The wave forms, the radiated energies and angular momenta at infinity were computed, and extensively compared to previous results for different orbits (circular, elliptic, parabolic, zoom-whirl).

Focusing on radial fall, back-action has been included in the analysis solely in the last decade. It appears that the self-force during the fall plays an attractive role.

We have also investigated orbital evolution. Indeed, the ’Capra programme’ targets non-adiabatic motion in strong regime as one of the main scientific achievements. The most emblematic non- adiabatic problem in gravitation is represented by radial fall. The proper computation of radial fall requires a self-consistent, i.e. iterative, approach for which the geodesic is continuously corrected by the self-force. Our code implements an iterative osculating method to trace the perturbed motion in the background metric. The results are applicable to the Regge-Wheeler and de Donder (harmonic) gauges, due to the regular transformation between the two gauges in this specific case. We finally show the differences between the geodesic motion and the perturbed motion, with and without the iterative orbital evolution.

Peter Diener, Samuel Cupp, Roland Haas, Ian Vega and Barry Wardell [Slides] [Movie 1] [Movie 2]
Self-force loops
I will present results of simulations of a scalar charge in elliptical orbit around a Schwarzschild black hole. The simulations where performed in the time domain in full spatial 3D using the effective source approach. I will discuss the accuracy and consistency of the simulations by comparing with known results and comparing energy and angular momentum losses from the self-force itself and from fluxes through the horizon and $\mathcal{J}^+$ . I will introduce the concept of self-force loops; a novel way of presenting self-force data that we are still trying to understand and interpret.

Peter Zimmerman [Slides]
Combining the Gravitational and Scalar Self-forces
We will present early results of a study considering the effects of coupling between gravitational and additional (non-gravitational) field perturbations on the first-order equations of motion of a point-like particle. The particular scenario examined here is a minimally coupled massless scalar field similar to the setup of a Brans-Dicke type theory in the Einstein frame. We will argue based on the form of the propagators in the normal neighbourhood that the coupling between fields only contributes to the finite part of the force, suggesting that the singular fields are decoupled and can be regularized separately using standard methods. Finally, we'll present the leading order contribution to the self-force equation due to the coupling between the scalar and gravitational fields derived using techniques from effective field theory.

Priscilla Cañizares [Slides]
Osculating Evolution to Model EMRI Resonances
Recent works have shown that a small body's self interaction becomes particularly important near resonances. Resonances are caused when the two (the radial and the polar) orbital frequencies become commensurate, that is, when some linear combination of these orbital frequencies with integer coefficients vanishes. On such resonant orbits, components of the back-reaction which normally average to zero over a full orbital period, instead combine coherently to substantially change their impact on the orbital evolution. This is because harmonics of the frequency that vanish on resonance, actually contribute to the secular component of the change in the orbital elements on resonance, but average to zero for off-resonance orbits.

I will review the osculating elements formalism, and introduce the work-in-progress that I am currently developing towards an application to the action-angle representation of the geodesic evolution. The key point of such a scheme is that the orbital frequencies appear in the osculating equations of motion, providing a direct way of estimating and studying the effect of resonances in gravitational wave emission.

Seth Hopper [Slides]
Eccentric bound motion on Schwarzschild: Self-force in a modified Regge-Wheeler gauge
We consider bound, eccentric motion of a point particle about a Schwarzschild black hole. Solving the field equations in Regge-Wheeler gauge yields solutions that are singular mode-by-mode at the location of the particle. We show how, with a simple gauge transformation these singularities can be avoided and the self-force can be computed.

Shahar Hadar [Slides]
A theory of post-Newtonian radiation and reaction
We address issues with extant formulations of dissipative effects in the effective field theory (EFT) which describes the post-Newtonian (PN) inspiral of two gravitating bodies by (re)formulating several parts of the theory. Novel ingredients include gauge invariant spherical fields in the radiation zone; a system zone which preserves time reversal such that its violation arises not from local odd propagation but rather from interaction with the radiation sector in a way which resembles the balayage method; 2-way multipoles to perform zone matching within the EFT action; and a double-field radiation-reaction action which is the non-quantum version of the Closed Time Path formalism and generalizes to any theory with directed propagators including theories which are defined by equations of motion rather than an action. This formulation unifies the treatment of outgoing radiation and its reaction force. We demonstrate the theory in the scalar, electromagnetic and gravitational cases by economizing the following: the expression for the radiation source multipoles; the derivation of the leading outgoing radiation and associated reaction force such that it is maximally reduced to mere multiplication; and the derivation of the gravitational next to leading PN order. In fact we present a novel expression for the +1PN correction to all mass multipoles.

Soichiro Isoyama [Slides], Takahiro Tanaka [Slides]
Adiabatic evolution of the constants of motion of an ispiral without and with resonance
We discuss the adiabatic evolution of the constants of the motion of a point mass inspiralling into a background Kerr spacetime, including resonance inspirals.

The first part of the talk (by Takahiro Tanaka) is dedicated to review the method to compute the long time averaged change rate of constants of motion for a non-resonance insipral, based on the Teukolsky formalism in frequency domain. Although there is no conserved current composed of the perturbation field corresponding to the Carter constant, it has been shown that the averaged rate of the change rate can be given by a simple formula with the aid of the radiative metric perturbation defined by half-retarded minus half-advanced perturbed field.

However, this formula essentially assumes that there exists a simultaneous turning point of the radial and polar oscillations. The problem is that the turning point is failed to exists if an inspiralling orbit crosses a resonance point, where the frequencies of these oscillations are in a rational ratio.

Then, in the second part of the talk (by Soichiro Isoyama), we show that how we can extend our strategy to compute the averaged rate of the change of the Carter constant for a resonance inspiral. By contrast to the non-resonance insipiral, we need to to treat the diverging retarded perturbed field directly. Nevertheless, since the change of the Carter constant only requires the long time averaged value of the specific components of the self-force, the regularization of the retarded field can still be achieved via a variant of the practical mode-sum regularization with the spheroidal harmonics. With the aid of this mode sum regularization and the scheme that enables us to reconstruct the metric perturbation from the Teukolsky's curvature variables, we show that the Teukolsky formalism still enables us to compute the averaged rate of the change of the Carter constant even in the resonance case without the direct self-force calculation.

Thomas Osburn [Slides]
Direct Integration of Lorenz Gauge Equations in the Frequency Domain: Fully Constrained EHS Method
We calculate the metric perturbation in Lorenz gauge but reduce the system of ODEs in size from ten to six equations using the four Lorenz gauge conditions. The method of extended homogeneous solutions is applied, with the homogeneous solutions to this smaller system automatically satisfying the Lorenz gauge conditions. The remaining four metric perturbation amplitudes are recovered algebraically from the constraints. The reduced size of the system of equations provides an increase in accuracy. We also examine static modes, low order modes, and calculation of the self force.