Current Research Activities
I am an applied mathematician by training, interested in the application of any mathematical tool to any problem of practical interest, especially the difficult ones. My research has always been in the area of Multiphase Flows. However, this is a very broad area, so the particular topics of interest change from time to time. Below I summarize some current areas of interest.
Droplet Impact - Modelling
Droplet impact is an important topic with many practical applications, ranging from spray cooling to bloodstain pattern analysis and Forensic Science.
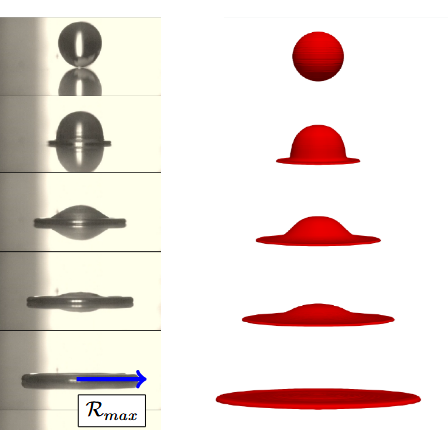The current focus of my modelling work is to understand such droplet impacts in the rim-lamella regime. This is a very special
regime of droplet impact where the droplet retains axisymmetry after impact. The impacts take place on extremely short timescale (of the order of milliseconds) and
can be visualized by a high-speed camera. The image on the left was taken with a Chronos 1.4 high-speed camera, with corresponding computer simulations of the same setup shown alongside.
This composite was created by a Theoretical Physics student as part of a final-year project.
The flow in the rim-lamella model can be described using a set of simplified ordinary differential equations. In general, these equations do not have analytical solutions, and the aim of my work is to use techniques from Applied Analysis to understand how the maximum spreading radius scales with Reynolds and Weber numbers.
Multiphase Flows - Simulation
To properly understand a fluid phenomenon, theory, modelling and simulation are required, all working together to shed light on a particular flow.
For these purposes, I have developed a parallel two-phase levelset solver (TPLS) to simulate extremely non-linear interfacial evolution in three-dimensional channel flows. This code has been greatly extended by collaborators at the Edinburgh Paralle Computing Centre to account for phase change and contact-line motion.
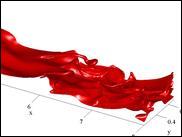
I also use standard CFD solvers such as OpenFOAM for simulation work. Below for example I show a simulation of a wave on an air-water interface, which was done using OlaFlow, in OpenFOAM. Using OpenFOAM (and its various add-ons) in this way can be very handy, as it sidesteps the coding and helps the reseracher to focus on the Fluid Dynamics. It is always important however to check using theoretical models that the simulations make sense, since CFD solvers are a bit of a "black box".
Film Spreading
I have always liked the Thin-Film Equation, for its analytical tractability. I have spent a number of years investigating a novel regulariztaion of the thin-film equation in case of contact-line flows. I have stumbled across a particularly nice regularization called the Geometric Thin-Film Equation. This has led to a very frutiful collaboration with Dr Richard Smith where we have looked at weak solutions of this particular equation. The weak solutions are not functions as such but are instead Radon Measures.
I am looking forward to this work having applications in computaitonal simulations of thin-film flows, where a clever regularization can speed up the calculations and help researchers to understand fluid flow in industrial applications such as in coatings and adhesives.