CFD codes - overview
Presented below are three open-source codes that I have developed for simulation and analysis of both single-phase and two-phase flows. The first one is called TPLS, and is a CFD solver that solves the two Navier-Stokes equations with level-set interface capturing methodology, using parallel MPI computing and coded in Fortran 90. The second code is a pared-down version of TPLS called S-TPLS. The "S" is for "Simplified". This version actually solves a single-phase version of the equations, incorporating an LES eddy viscosity. It can be used for demonstration, teaching, or reserach purposes. It is a useful springboard into the world of TPLS. Finally, the third code here is really a suite of Matlab codes for doing transient-growth calculations for the linear instability of two-phase stratified flows.
Two-phase levelset code (TPLS)
TPLS (Two-Phase Level Set) is a Computational Fluid Dynamics code developed by me and Dr Prashant Valluri of the University of Edinburgh's School of Engineering. It simulates the interface between two fluid phases, a phenomenon with a number of industrial applications including oil and gas hydrate transport, cleaning processes, distillation/absorption, and evaporative cooling of microelectronics.
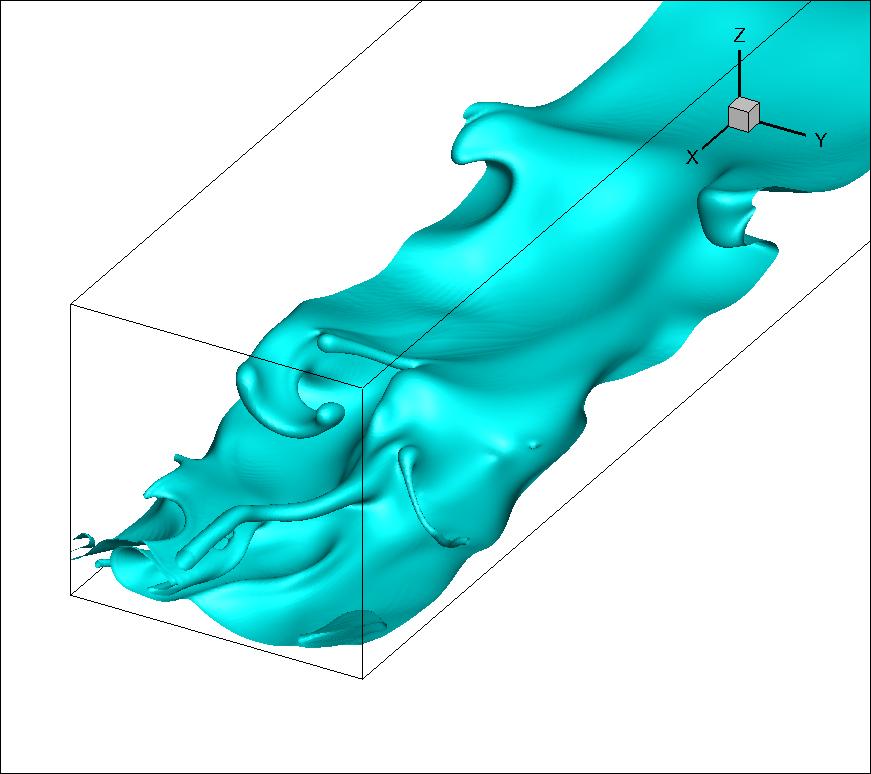
To do this, the code solves the two-phase Navier-Stokes equations with levelset interface capturing technology. Even for scenarios where the bulk flow is laminar, the interfacial structures are quite complicated, and high-resolution simulation in three dimensions are required. These simulations can only be performed in a realistic timeframe on supercomputers. Thus, TPLS is fully parallelized for execution on machines with thousands of cores. A 2D MPI process decomposition coupled with a hybrid OpenMP parallelisation scheme allows scaling to 1000s of CPU cores.
The code has been rigorously validated with respect to Orr-Sommerfeld, Orr-Sommerfeld-Squire, and Stuart-Landau semi-analytical theories, for a wide range of Reynolds numbers, viscosity ratios, density ratios, capillary numbers, etc., as described here. The code can be configured in co-current, countercurrent, horizontal, and vertical cases, with inlet/outlet boundary conditions or periodic boundary conditions. Currently we are restricted to channel geometries, but would like to include pipe geometries at a lager stage.
In 2012 Prash and I received funding from the HECToR dCSE scheme and the EPSRC to improve the performance and scalability of the code. The development work was carried out by Dr David Scott of the Edinburgh Parallel Computing Centre (EPCC), and we were able to achieve speedups of over 50% in the pressure solver (the most expensive part of the code) by replacing the bespoke Jacobi/SOR solver with Krylov Subspace methods from the PETSc library, and by optimising the existing use of MPI and OpenMP in the code. A second Archer dCSE award in 2014 funded Dr Toni Collis of the EPCC to carry out other substantial improvements, in particular parallel I/O using the NetCDF format for the output data files. Further work funded by the Software Sustainability Institute (and carried out by Mike Jackson of the EPCC) has led to a working version of the code that is more customizable and user-friendly to allow use by other research groups. All of these projects have been supervised ably by Iain Bethune, a project manager at the EPCC.
To allow other research groups to benefit from our research and code development, we have released this developed version of the TPLS code on Sourceforge under the Open-Source BSD License.
S-TPLS
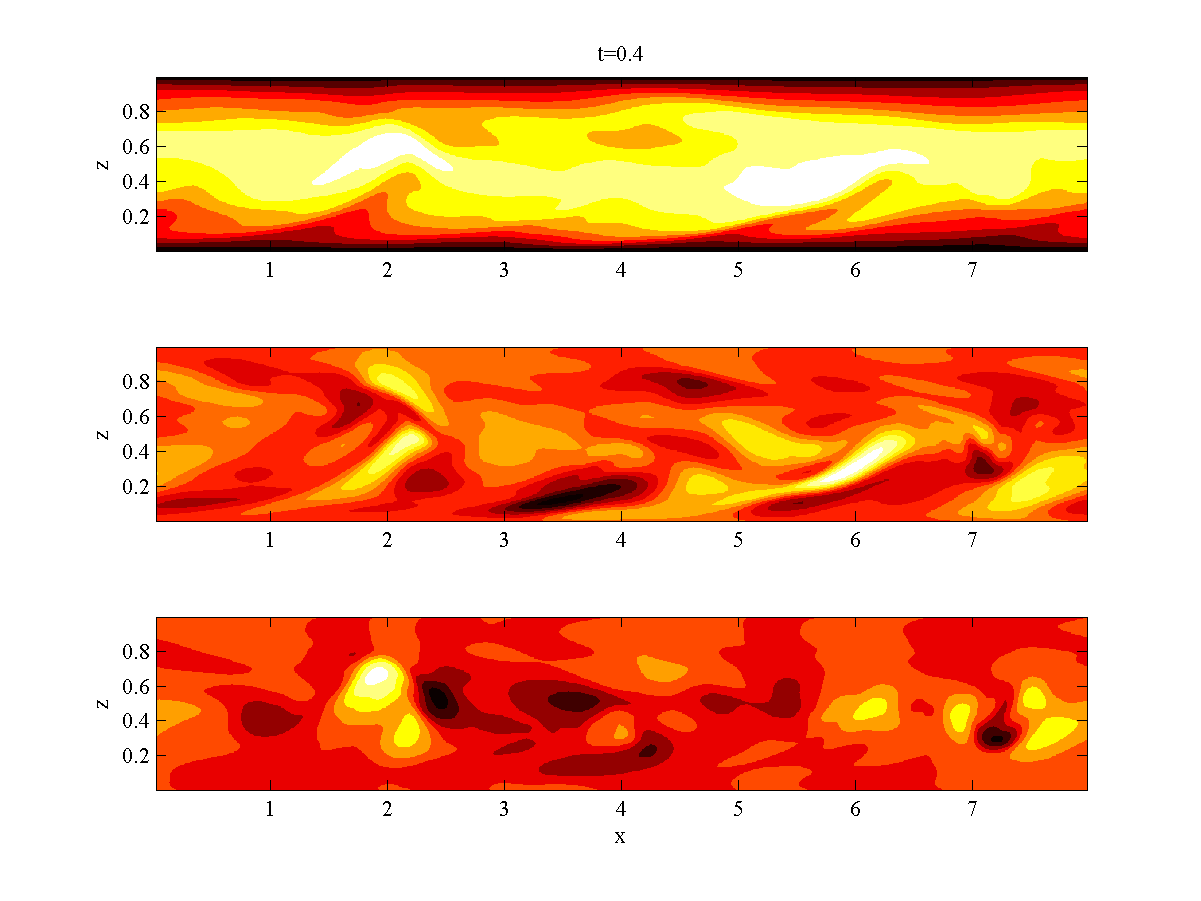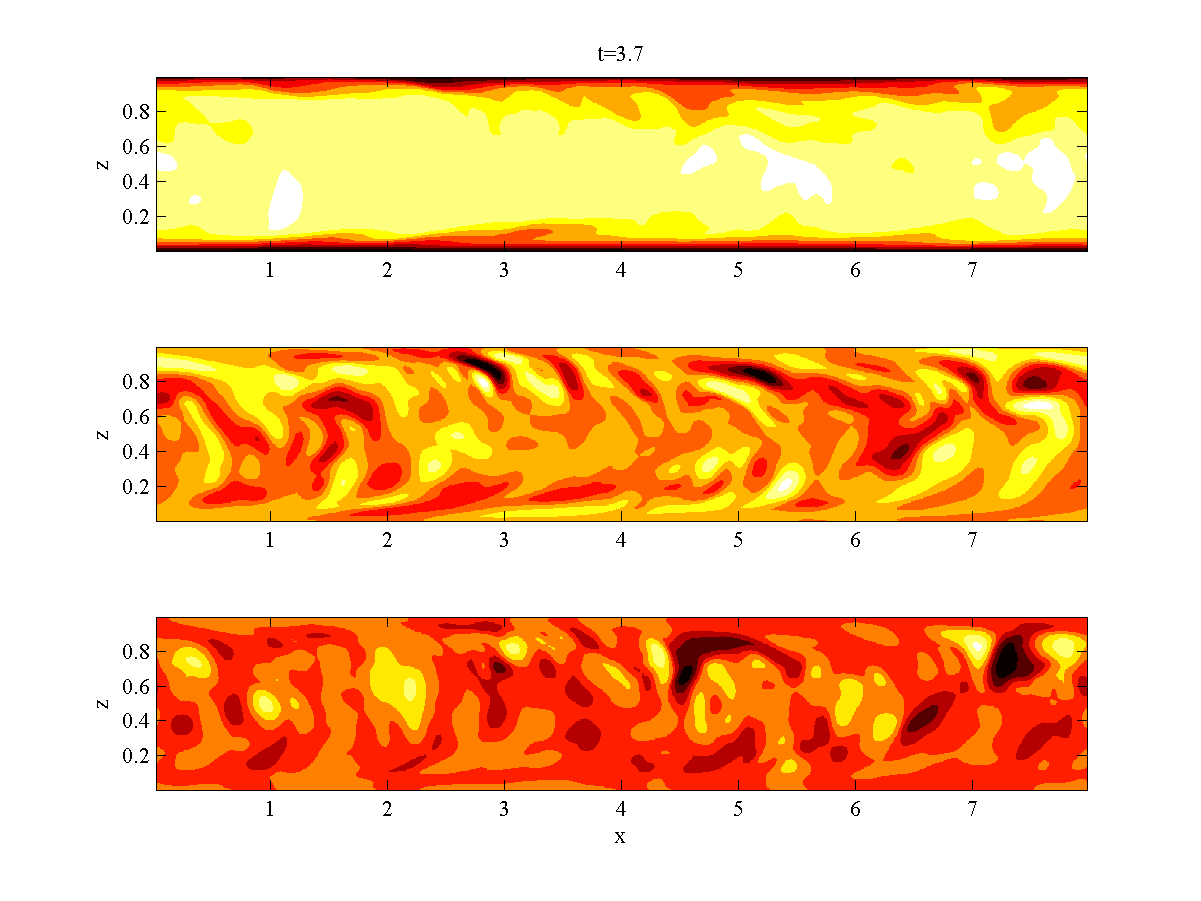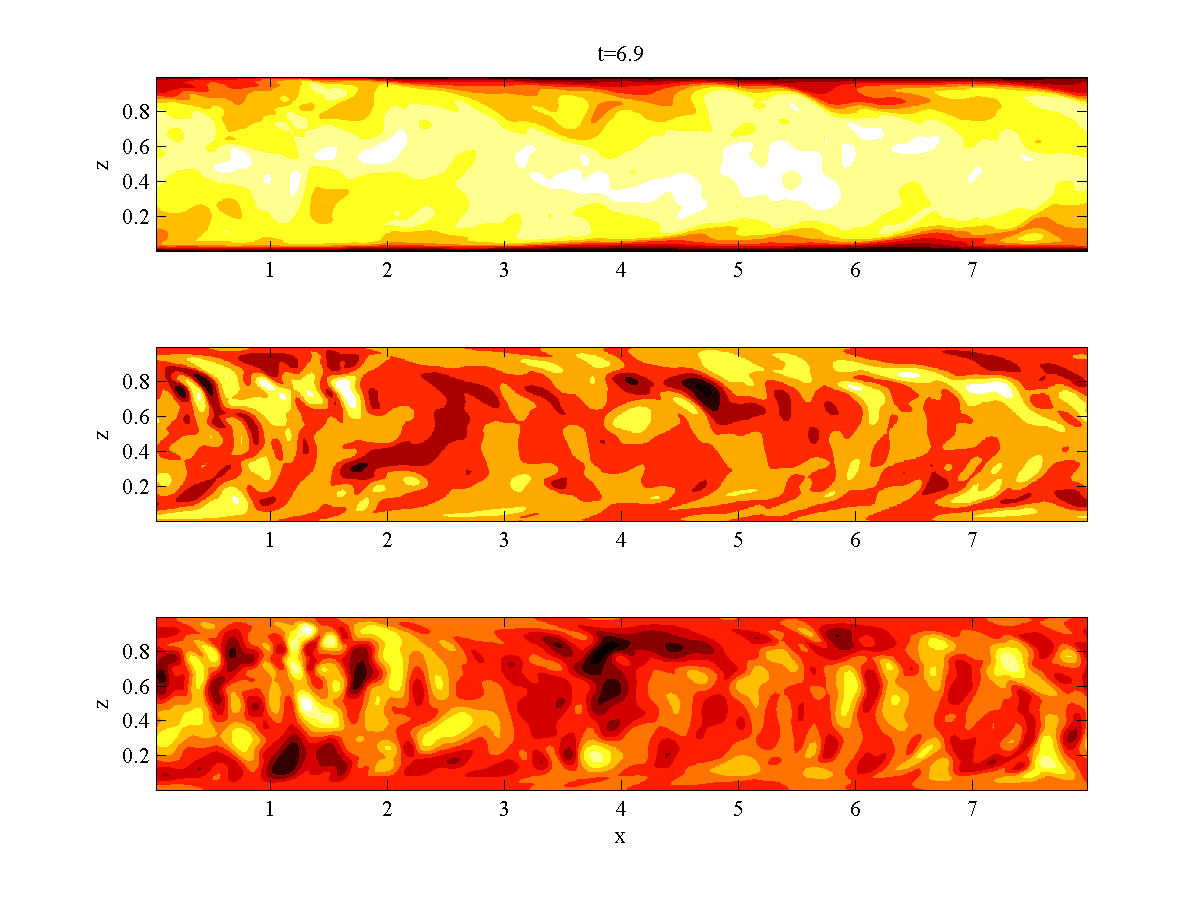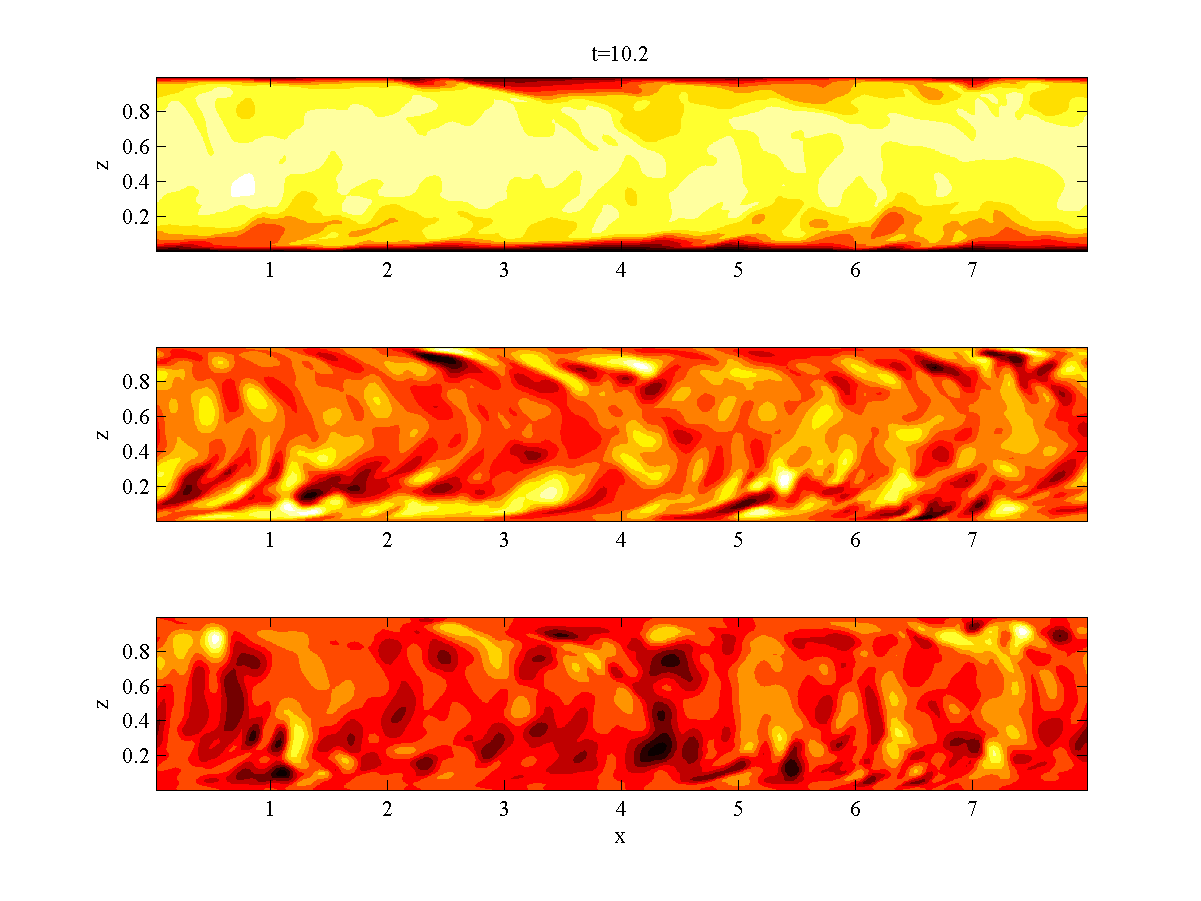
A pared-down single-phase version of the TPLS code (S-TPLS) is available for demonstration and teaching purposes. The aim of S-TPLS is to introduce a new emphasis on coding and physics in CFD education - instead of the more traditional "black-box" approach involving commerical computational packages. An article about this mission and the S-TPLS code is available here. S-TPLS is available for download:
Sample simulation results from S-TPLS appear on the left. These correspond to a large-eddy simulation of single-phase pressure-driven channel flow. Animations of a planar slice are shown, corresponding to the streamwise, spanwise, and wall-normal velocities. The plane is extends in the streamwise and wall-normal directions.
Transient-growth calculations in Matlab
An equilibrium configuration of a two-phase channel flow is unidirectional two-phase Poiseuille flow, wherein the phases are confined in two layers parallel to the direction of flow. We use linear theory to study the early-time development of three-dimensional disturbances: the stability of the basic Poiseuille flow to small-amplitude disturbances is investigated by solving the linearized equations of motion in the disturbance velocity and pressure fields. Using eigenvalue analysis and the linearized equations of motion for a reduced set of variables (the wall-normal velocity and vorticity), it can be shown that the small-amplitude disturbances grow or decay exponentially, with growth rates and phase speeds determined from a modal Orr--Sommerfeld--Squire (OSS) eigenvalue analysis.
The eigenvalue problem only gives the asymptotic solution of the associated initial-value problem, valid for very late times - corresponding to "picking out" the most-dangerous mode from the eigenvalue analysis. However, at finite times, a combination of modes can combine to produce transient growth rates in excess of the asymptotic most-dangerous exponential growth rate. This is possible because the eigenfunctions of the OSS equation are non-orthogonal, which is due in turn to the non-normality of the operators in the same equation. This is a famous result of Trefethen and co-workers. Therefore, transient growth calculators to optimize the energy norm (in a standard fashion) are presented here for use by other researchers, available under a BSD license.
A companion document to accomapny these codes is available here.