Advanced Fluid Mechanics (10 ECTS ACM 40740, 5 ECTS ACM 40890)

Description: This module introduces advanced concepts and methods in Fluid Dynamics. There are two versions: ACM 40740 for 10 ECTS and ACM 40890 for 5 ECTS. The course material is the same for both module codes; the only difference is the level of coursework required: this is much greater for ACM 40740 than for ACM 40890.

 

 

The main focus is on viscous incompressible flows, under the following broad headings:

  • Canonical examples of fluid instability: Eigenvalue analysis of linear instability in the Rayleigh-Benard, Rayleigh-Taylor, and Kelvin-Helmholtz systems. Eigenvalue analysis of parallel flow instability leading to the Orr-Sommerfeld equation.
  • Parallel flow instability beyond the temporal theory: Absolute and convective instability, transient growth
  • Weakly nonlinear stability theory: Stuart-Landau theory applied to the Cahn-Hilliard and Kuramoto-Sivishinsky equation
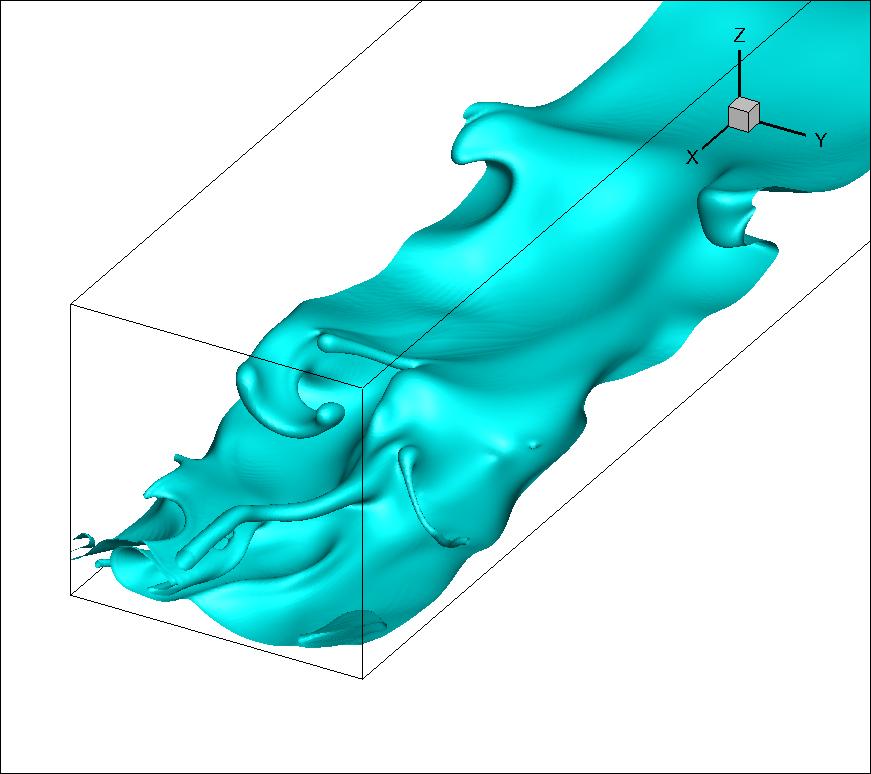
  • Turbulence: Problems in turbulence. Kolmogorov spectra. Wall-bounded turbulence and Reynolds averaging. Closure models. Discussion of direct numerical simulation and large-eddy simulation. The notion of wall-functions in large-eddy simulation.
  • Introduction to High-Performance computing: Solving sparse linear problems iteratively. Applications of such methods to Computational Fluid Dynamics. Introduction to multithread and multicore programming in Fortran.

On completion of this module students should be able to

  • Write down the eigenvalue problem for the canonical physical systems of Fluid Dynamics
  • Derive the Orr-Sommerfeld equation and compute exact solutions in certain cases
  • Describe the subtle features of linear stability theory beyond temporal eigenvalue analysis
  • Carry out a Stuart-Landau analysis on simple nonlinear equations
  • Characterize turbulence using the Kolmogorov and Reynolds-averaged theories.
  • Solve sparse linear problems iteratively and implement their solution in Fortran.

In addition to the study of sparse linear systems and their role in Computational Fluid Dynamics, a number of mini computational projects will form part of this module. Therefore, on completion of this module students should gain much familiarity with numerical and computational methods in fluids. In particular, students should further be able to

  • Perform an Orr-Sommerfeld stability analysis of Poiseuille flow using spectral methods in Matlab
  • Implement an existing parallel flow solver to study large-eddy simulations in turbulent channel flow
  • Analyse the turbulent statistics emanating from simulations such as the above

Module philosophy: As this is a graduate-level module, heavy emphasis is placed on independent study. There will be at most two lectures per week. Thus, not all of the material in the lecture notes will be covered in class. Your independent study will be guided by reading this material, supplementary material from the recommended textbooks, and by the exercises contained in the lecture notes.

Course documents:

Computer code