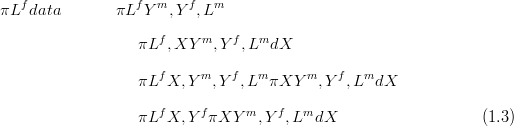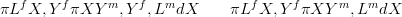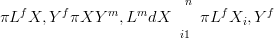Highly multivariate statistical problems may lead to slow inference procedures. One example of such a problem involves palaeoclimate reconstruction from fossil pollen data, which is an example of an inverse problem. Existing explorations of this challenging area of study often involve a trade off between model complexity and speed of inference. Fast approximate Bayesian inference methods offer a solution. In addition, an extension of the methodology allows for model validation to be performed quickly for the inverse problem. Conversely, the large scale of the palaeoclimate project offers a real challenge to the emerging approximate inference engine.
The Royal Statistical Society read paper “Bayesian Palaeoclimate Reconstruction”, Haslett et al. (2006) presented work on high resolution pollen based reconstruction of the palaeoclimate at a single location since the last ice-age. This paper outlined the basic concepts involved in performing fully Bayesian inference on unknown climates given modern and fossil pollen data and modern climatic data. The work was a detailed “proof of concept”; extensions and improvements to the statistical methodology were considered, both in the paper and in the subsequent printed discussion.
The main crux of the methodology in that work was acknowledged to be computational; indeed the computational burden imposed compromises on the modelling. The work presented herein represents extensions in the statistical methodology and advances in the computations involved as developed by the author. These contributions are outlined in Section 1.4.
The Bayesian palaeoclimate reconstruction project is an ongoing initiative to build upon existing classical approaches to the reconstruction of prehistoric climates, using fossil pollen data. Specifically, the project seeks to handle all uncertainties quantitatively and coherently in a fully Bayesian framework and to combine different types of information to reduce these uncertainties.
The primary dataset for the palaeoclimatology reconstruction project is the RS10 dataset of Allen et al. (2000). A collection of modern pollen surface sample counts Y m y1m,…,yMm ;M 7742 are taken from the uppermost 5 to 10mm of lake bed sediment at numerous locations in the northern hemisphere. Along with covariates in the form of local contemporary climate measurements Lm, they comprise the modern dataset. This is also referred to as the training data. Sample fossil pollen counts Y f are extracted from cores taken from lake or mire sediment. Measures of the prehistoric climate variables Lf at the time of deposition of these fossil pollen spores are unknown; the central premise of palynological palaeoclimate reconstruction is that these climates may be inferred from the pollen data, albeit with some uncertainty. Both the modern and fossil pollen data comprise counts of numerous plant types (taxa; see below). There is therefore a vector of counts reported at each sampling location. The length of this vector is equal to the number of distinguishable pollen spore types.
Reconstruction of past climates involves using a multivariate regression type model in which the proportion of the ith species in the training pollen data set yim is an indirect observation of a latent “response” to the corresponding modern climate variables Lm. This response is defined as the propensity to contribute pollen to the dataset in the given climatic conditions and is modelled as a smooth function of climate, fitted by reference to the pollen counts data. At the first stage, the training data is used to calibrate the model for the response of vegetation to climate. At the second stage, the regression is “inverted” and applied to assemblages of fossil data, which yields a quantitative reconstruction of climate. The two stages are referred to as the forward and the inverse parts of the model respectively. This is known as the response surface method.
Huntley (1993) argues that at least some species may have multiple optima and hence the response function may be multimodal. Non-parametric modelling of the response function is therefore advocated. This is due at least in part to the fact that the pollen data is in fact sorted into plant “taxa” rather than individual species. Each taxon consists of one or more species; sometimes an entire genus or even an entire family comprising several plant species are categorized simply as a single taxon. A given taxon may then contain multiple species that thrive and fail at dissimilar climates. This is because the pollen data are categorized visually and multiple related species frequently produce pollen spores that are indistinguishable to the eye.
There is a considerable literature on palaeoclimate reconstruction from such palynological data using the response surface methodology in the botany community (see for example Bartlein et al. (1986), Huntley (1993) and Allen et al. (2000)). These reconstructions use various estimation methods, essentially attributing to a fossil pollen assemblage the modern climate that has the “closest” matching pollen assemblage.
The main disadvantage of the classical methods is that there is no consistent way to make statements of uncertainty in the reconstructions. There are other serious issues; for example the RS10 (response surface 10) method of Allen et al. (2000) finds the 10 climates that correspond to the fitted responses that are closest to the fossil pollen assemblage. These climates are then averaged and the average is returned as the estimated palaeo-climate. A crude measure of uncertainty is also reported as the “average chord distance”; the average distance between the vector of fossil pollen proportions and the vectors that are derived from the fitted response surfaces. An immediate problem occurs as a result of this simplified analysis. For example, tundra and steppe vegetation can produce very similar pollen assemblages, yet occur under very different climatic regimes. For a given fossil pollen assemblage, some of the 10 closest modern day responses may be steppe and some tundra; the averaged corresponding climates will lie in between in the climate space. This reconstructed climate may be in a region of climate that does not produce pollen assemblages anything like the fossil assemblage; it may even correspond to a climate that simply does not occur.
Unlike the classical approach, the Bayesian paradigm deals with all sources of uncertainty
in a coherent manner. The unknown statistical parameters X are treated as random
variables and a likelihood function π
Y SX is used to express the relative probabilities of
obtaining different values of this parameter when a particular dataset Y has been
observed. Prior probability densities πX are placed on the unknown parameters
to reflect any subjective beliefs held before observation of data. The posterior
density πXSY is delivered via Bayes theorem; it is a normalised product of the
prior and likelihood densities and reflects the updated beliefs in light of the
data.
Bayes theorem constructs the posterior density πXSY which is a summary of all
knowledge about the parameter X subsequent to observing Y . The posterior distribution
is a comprehensive inference statement about the model variables X. Any summary of the
posterior distribution is useful e.g. moments, quantiles, highest posterior regions and
credible intervals.
The Bayesian model presented in Haslett et al. (2006) is briefly described next. The forward stage of the model infers the latent response of vegetation to climate given the modern pollen counts and corresponding modern climate data. The inverse stage then uses knowledge of the latent responses to infer climate from fossil counts data.
In this stage of the inference, the modern training data of pollen counts and associated climatic data are used to inform probabilistic statements on the unobservable response of vegetation to climate. The vectors of pollen counts at each location are modelled as indirect observations of the unknown responses 1 to the climate at that location. Building upon the notation already used in this section, the responses are labeled X There is a vector of X responses at each point in the climate space, one for each taxon. Each individual taxon then has a set of responses across the climate space referred to as the taxon response surface; jointly over all taxa these are denoted by X.
Bayes theorem is used as above to construct the posterior for the response surfaces given the modern data, Y m,Lm .
 | (1.2) |
The integral in the denominator is typically not tractable analytically. In Haslett et al. (2006) numerical integration was performed approximately using a Metropolis-Hastings Markov Chain Monte Carlo algorithm.
The second stage of the Bayesian inference procedure is the calculation of posterior
probability distributions on the unknown palaeoclimates Lf, given the posterior for the
latent surfaces πXSY m,Lm (derived in the first stage of the model) and the fossil pollen
counts Y f. This is the inverse problem (also known as multivariate non-linear calibration;
ter Braak discussion of Haslett et al. (2006)).
Sampled responses X are passed to an MCMC algorithm for sampling from the posterior for palaeoclimate Lf given fossil pollen Y f and the surfaces X.
As the fossil pollen counts alone (without knowledge of the climate at which they
occurred) contribute little, or even no, information to the posterior for response surfaces
given data, πXSY m,Lm,Lf is approximately equal to πXSY m,Lm :
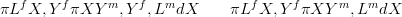 | (1.4) |
The fully Bayesian approach is to solve the left-hand side of Equation (1.4); the right-hand side is an approximation that is common to most inverse problems.
In fact, a positive feedback mechanism may occur if the fossil counts are left in Equation (1.4); removing them may in fact lead to a more accurate fit. This is referred to as “cutting feedback”; Rougier (2008) states that cutting feedback, although technically a violation of coherence, may be presented in terms of best-input. The model is trained using only the data about which the analyst is confident.
Essentially, fitting the responses using the modern training data, for which counts and climates are available, and the fossil data, for which counts only are available, may lead to unwanted positive feedback due to the fossil counts. The model training will begin by placing fossil counts in a region of climate space; given this selected region, the response surface appears to fit well. But the response surface was built using those counts in that region. The initial choice has been strengthened, despite the fact that is was an arbitrary choice. Training the model only on the modern data, for which climate is known, is preferred for this reason.
Integration over the latent surfaces was via Monte Carlo integration in Haslett et al. (2006): samples Xi,…,Xn are drawn from the posterior using the first stage (forward problem) and passed to the second stage (inverse problem):
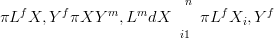 | (1.5) |
An alternative to MCMC for this task is proposed in this thesis. Namely, the suite of approximation techniques referred to as INLA are applied and expanded for this purpose. The implications of imposing any new modelling procedures and algorithms on the forward stage are considered primarily in terms of the impact on the inverse stage.
The most pressing challenges encountered in the Bayesian palaeoclimate project to date involve the intensive computations necessary to carry out inference on the parameters of interest. This is due mainly to an over-reliance on the computationally intensive Markov Chain Monte Carlo algorithm. The large number of parameters required in the complex modelling leads to serious concerns about the mixing the algorithm achieves in the unknown parameter space. Linked to this is the problem that convergence is far from assured, even after runs of the order of weeks (see Haslett et al. (2006)). Additional detail in the model is prohibited due to memory and computation concerns.
As discussed briefly in Section 1.1.1, the unobservable response surfaces must be modelled non-parametrically. One way to achieve this is by discretising climate space on a regular grid and modelling the response as a random variable at each node. High resolution is desirable, requiring the use of a very fine discrete grid on the climate variable space. This results in a very large number of latent variables. The paper Haslett et al. (2006) dealt with a model including the order of 104 unknowns; and this is for a inference performed on a greatly reduced dataset using a simplified model.
A brief outline of the research presented by chapter in this thesis follows.
A brief review of the literature on palaeoclimate reconstruction is presented. Progress towards the standard set by Haslett et al. (2006) is charted and Bayesian statistical methods for inverse inference are summarised. The remaining weaknesses in the current methodology are outlined and the techniques used to overcome these in this thesis are introduced.
In order to separate modelling issues from issues of inference in the forward problem, this chapter focusses on models with known parameters. Various model choices and the implications of these choices are presented. Some new statistical models are detailed. The novel contributions of this chapter are the methods for determining the decomposability of large, multivariate models into separate, independent modules and the nested compositional model. Issues related to the decomposition of models are introduced and discussed.
The single biggest reduction of the computations required for a full Bayesian inference to be performed on the palaeoclimate dataset are due to the approximation techniques presented in this chapter. By approximating the posterior for the unknown variables in the forward problem with a tractable multivariate density, Markov Chain Monte Carlo may be avoided entirely. The posterior distribution for the responses may be expressed analytically and thus issues regarding mixing and convergence are avoided. The approximation error is typically lower than the Monte Carlo error and the computations required are dramatically reduced. This allows for the addition of extra detail to the model and dramatically increases the potential of the application of the procedure to larger datasets, examples of which are explored.
There are many modelling choices made throughout the application in Chapter 6. These choices must be supported and alternatives explored. Cross validation is a useful tool in evaluating the fit of the Bayesian models to the data. This is typically done by computationally intensive Markov Chain Monte Carlo; it requires many repeated runs and, for large problems such as the palaeoclimate reconstruction project, this may become computationally overwhelming and is therefore not considered. Approximation methods are once again discussed in this context along with further application to the pollen / climate dataset.
An investigation is carried out into the implications of decomposing the counts data vectors and carrying out marginal inferences on each component of the vector sequentially. This is at best identical to a joint inference on all components at once and at worst an approximation to it. The accuracy of the approximation is expressed as a function of several impacting factors and the conditions for exact reproduction of the joint posterior from the marginal posteriors (perfect decomposition) are described.
Details related to performing inference using the techniques already developed in previous chapters are presented. This chapter serves as a platform towards the application to real data in Chapter 6.
The motivating problem for the research conducted in this thesis is to improve and advance the palaeoclimate reconstruction project. Therefore, a chapter is devoted to applying the work developed in previous chapters to the RS10 pollen and climate dataset. The various approximation algorithms allow for a richer modelling of the forward problem (the response of vegetation to climate) than was previously possible. The modelling of zero-inflation represents a fundamental change in the model. Practical issues regarding the application of the new model and use of the approximations are identified and discussed. Results are presented and compared with the results derived from previous approaches. A fast cross-validation methodology for the inverse problem is central to this chapter.
The results from the preceding chapters are summarised and discussed. An appraisal of the work to date is conducted and outstanding issues and challenges are identified. Solutions to these remaining challenges are suggested and alternative methodologies briefly outlined.
The following is a statement of the main contributions to the palaeoclimate reconstruction project by the author as presented in this thesis:
