Warning: Undefined array key "do" in /home/levene/public_html/w/mst10030/lib/plugins/revealjs/action.php on line 14
Table of Contents
Linear equations in 3 variables
Definition
If $a,b,c,d$ are any fixed numbers, then equation \[ ax+by+cz=d\] is a linear equation in 3 variables.
When you draw the set of all solutions of a linear equation in 3 variables, you always get a plane in 3-dimensional space, $\mathbb{R}^3$.
Examples
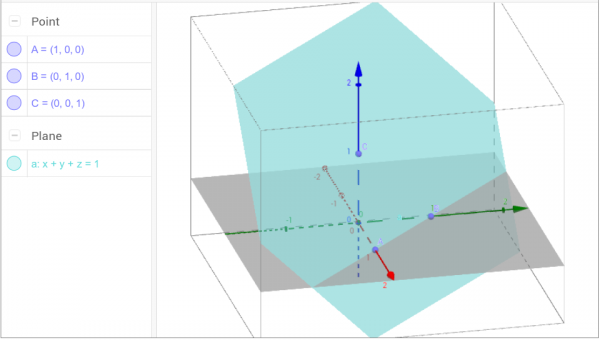
- $x+y+z=1$
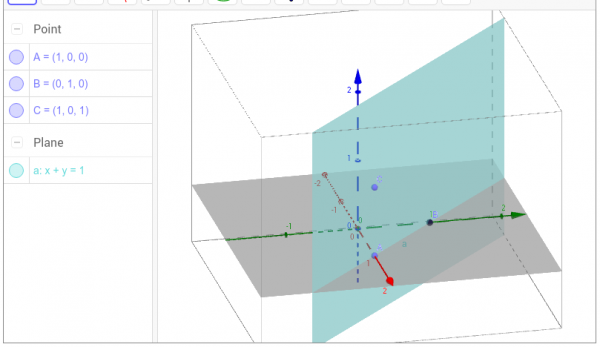
- $x+y=1$ This may be viewed as a linear equation in 3 variables, since it is equivalent to $x+y+0z=1$.
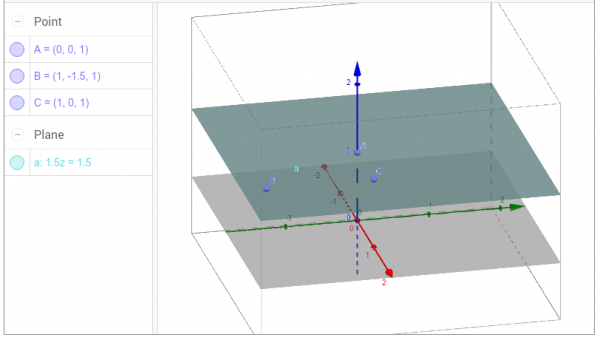
- $z=1$, viewed as the equation $0x+0y+z=1$
Linear equations (in general)
A linear equation in $m$ variables (where $m$ is some natural number) is an equation of the form \[ a_1x_1+a_2x_2+\dots+a_mx_m=b\] where $a_1,a_2,\dots,a_m$ and $b$ are fixed numbers (called coefficients) and $x_1,x_2,\dots,x_m$ are variables.
Example
\[ 3x_1+5x_2-7x_3+11x_4=12\] is a linear equation in 4 variables.
- A typical solution will be a point $(x_1,x_2,x_3,x_4)\in \mathbb{R}^4$ so that $3x_1+5x_2-7x_3+11x_4$ really does equal $12$.
- For example, $(-2,0,-1,1)$ is a solution.
- The set of all solutions is a 3-dimensional object in $\mathbb{R}^4$, called a hyperplane.
- Since we can't draw pictures in 4-dimensional space $\mathbb{R^4}$ we can't draw this set of solutions!
Systems of linear equations
A system of linear equations is just a list of several linear equations. By a solution of the system, we mean a common solution of each equation in the system.
Example
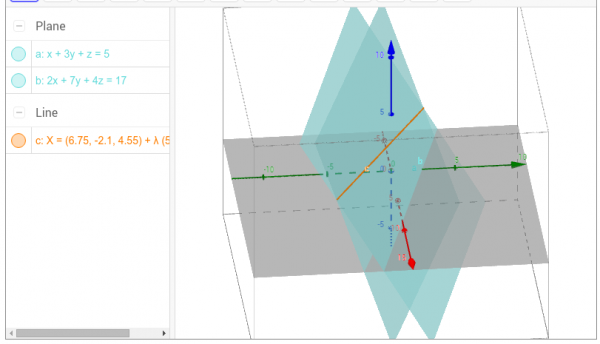
Find the line of intersection of the two planes $ x+3y+z=5$ and $ 2x+7y+4z=17$.
Intersection of $ x+3y+z=5$ and $ 2x+7y+4z=17$
- To find the equation of the line of intersection, we must find the points which are solutions of both equations at the same time.
- Eliminating variables, we get $x=-16+5z$, $y=7-2z$
- The line of intersection consists of the points $(-16+5z,7-2z,z)$, where $z\in\mathbb{R}$