MST10030 notes wiki

Last time

• Dot product: $\vec v\cdot\vec w=v_1w_1+v_2w_2+\dots + v_nw_n$
• Geometric formula: $\vec v\cdot \vec w = \|\vec v\|\,\|\vec w\|\,\cos\theta$
  • $\|\vec v\|=$length of $\vec v$ $=\sqrt{v_1^2+\dots+v_n^2}$
  • $\|\vec w\|=$length of $\vec w$ $=\sqrt{w_1^2+\dots+w_n^2}$
  • $\theta=$angle between $\vec v$ and $\vec w$
• $\vec v$ and $\vec w$ are orthogonal (at right-angles) if $\vec v\cdot \vec w=0$

Orthogonal projection

Let $\def\pp{\vec p}\def\ww{\vec w}\def\vv{\vec v}\def\nn{\vec n}\ww$ non-zero, and $\vv$ any vector.

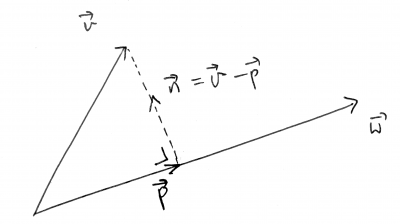
$\pp$ is the orthogonal projection of $\vv$ onto $\ww$ if:

1. $\pp$ is in the same direction as $\ww$; and
2. the vector $\nn=\vv-\pp$ is orthogonal to $\ww$.

• We write $\pp=\def\ppp{\text{proj}_{\ww}\vv}\ppp$.
• $\nn=\vv-\pp$ is called the component of $\vv$ orthogonal to $\ww$.

Formula for $\pp=\ppp$

• $\nn=\vv-\pp$ is orthogonal to $\ww$, so $\nn\cdot \ww=0$.
  • so $(\vv-\pp)\cdot \ww=0$
  • so $\vv\cdot\ww-\pp\cdot\ww=0$
  • so $\pp\cdot\ww=\vv\cdot\ww$
• $\pp$ in same direction as $\ww$, so $\color{blue}{\pp=c\ww}$ for some scalar $c$
  • so $c\ww\cdot \ww=\vv\cdot\ww$
  • so $c\|\ww\|^2=\vv\cdot\ww$
  • so $c=\frac{\vv\cdot\ww}{\|\ww\|^2}$.
• So $\color{blue}{\pp=\ppp=\frac{\vv\cdot\ww}{\|\ww\|^2}\ww}.$

Example

$\vv=\def\c#1#2#3{\left[\begin{smallmatrix}#1\\#2\\#3\end{smallmatrix}\right]}\c12{-1}$ and $\ww=\c2{-1}4$

• $\ppp=\frac{\vv\cdot\ww}{\|\ww\|^2}\ww$
  • $=\frac{2-2-4}{2^2+(-1)^2+4^2}\c2{-1}4$
  • $=-\frac4{21}\c2{-1}4$
• component of $\vv$ orthogonal to $\ww$ is $\nn=\vv-\ppp$
  • $\nn=\c12{-1}-\left(-\frac4{21}\right)\c2{-1}4=\frac1{21}\c{29}{38}{-5}$.

The cross product of vectors in $\mathbb{R}^3$

The standard basis vectors in $\mathbb{R}^3$

• Define $\def\i{\vec \imath}\i=\def\c#1#2#3{\left[\begin{smallmatrix}#1\\#2\\#3\end{smallmatrix}\right]}\c100$, $\def\j{\vec \jmath}\j=\c010$ and $\def\k{\vec k}\k=\c001$.
• These are the standard basis vectors of $\mathbb{R}^3$.
• Any vector $\vec v=\c{v_1}{v_2}{v_3}$ is a linear combination of these vectors
  • (that is, a sum of scalar multiplies of $\i$, $\j$ and $\k$)
• because\[ \def\vc#1{\c{#1_1}{#1_2}{#1_3}}\vec v=\vc v=\c{v_1}{0}{0}+\c{0}{v_2}{0}+\c{0}{0}{v_3} = v_1\i+v_2\j+v_3\k.\]

The cross product

• Let $\def\vc#1{\left[\begin{smallmatrix}#1_1\\#1_2\\#1_3\end{smallmatrix}\right]}\vec v=\vc v$ and $\vec w=\vc w$ be vectors in $\mathbb{R}^3$
• $\vv\times\ww$ is another vector in $\mathbb{R}^3$, the cross product of $\vv$ and $\ww$
• … defined as the determinant $\color{blue}{\vv\times\ww=\def\cp#1#2#3#4#5#6{\left|\begin{smallmatrix}\i&\j&\k\\#1&#2&#3\\#4&#5&#6\end{smallmatrix}\right|}\def\cpc#1#2{\cp{#1_1}{#1_2}{#1_3}{#2_1}{#2_2}{#2_3}}\cpc vw.}$
• Interpret this by Laplace expansion along row 1:\[\cpc vw=\def\vm#1{\left|\begin{smallmatrix}#1\end{smallmatrix}\right|}\vm{v_2&v_3\\w_2&w_3}\i-\vm{v_1&v_3\\w_1&w_3}\j+\vm{v_1&v_2\\w_1&w_2}\k=\c{v_2w_3-v_3w_2}{-(v_1w_3-v_3w_1)}{v_1w_2-v_2w_1}\]

Example

Let $\vv=\c13{-1}$ and $\ww=\c21{-2}$.

• $\vv\times \vv=\cp13{-1}13{-1}=\c000=\vec0$
• $\vv\times\ww=\cp13{-1}21{-2}=\c{3(-2)-1(-1)}{-(1(-2)-(-1)2)}{1(1)-3(2)}=\c{-5}0{-5}$
• $\ww\times\vv=\cp21{-2}13{-1}=\c{1(-1)-(-2)3}{-(2(-1)-(-2)1)}{2(3)-1(1)}=\c{5}0{5}=-\vv\times\ww$

Example: cross products of standard basis vectors

We have \[ \i\times\j=\cp100010=\c001=\k,\] \[ \j\times\k=\cp010001=\c100=\i\] \[ \k\times\i=\cp001100=\c010=\j\]

Proposition: properties of the cross product

For any $\def\uu{\vec u}\uu$, $\vv$ and $\ww$ in $\mathbb{R}^3$ and any $c\in\mathbb{R}$:

1. $\uu\times(\vv+\ww)=\uu\times\vv+\uu\times\ww$
2. $\vv\times\ww=-\ww\times\vv$
3. $(c\vv)\times \ww=c(\vv\times\ww)=\vv\times(c\ww)$
4. $\vv\times\vv=\vec0$
5. $\vv\times \vec0=\vec0$
6. $\vv\times \ww$ is orthogonal to both $\vv$ and $\ww$

Proof

• Calculations/properties of the determinant.

Theorem: cross and dot product formula

For any vectors $\vv$ and $\ww$ in $\mathbb{R}^3$, we have \[ \|\vv\times\ww\|^2+(\vv\cdot\ww)^2=\|\vv\|^2\,\|\ww\|^2.\]

The proof is a calculation, which we leave as an exercise.

Corollary: the length of $\vec v\times\vec w$

For any vectors $\vv$ and $\ww$ in $\mathbb{R}^3$, we have \[ \|\vv\times\ww\|=\|\vv\|\,\|\ww\|\,\sin\theta\] where $\theta$ is the angle between $\vv$ and $\ww$ (with $0\le\theta\le\pi$).

Proof

• Geometric dot product formula: $\vv\cdot\ww=\|\vv\|\,\|\ww\|\cos\theta$
• $\times$ & $\cdot$ formula: $\|\vv\times\ww\|^2+(v\cdot w)^2=\|\vv\|^2\,\|\ww\|^2$
• So $\|\vv\times\ww\|^2=\|\vv\|^2\,\|\ww\|^2-(\vv\cdot\ww)^2$
  • $=\|\vv\|^2\,\|\ww\|^2-\|\vv\|^2\|\ww\|^2\cos^2\theta$
  • $=\|\vv\|^2\,\|\ww\|^2(1-\cos^2\theta)$
  • $=\|\vv\|^2\,\|\ww\|^2\sin^2\theta$.
• $\sin\theta\ge0$ for $0\le\theta\le\pi$, so taking square roots of both sides gives $ \|\vv\times\ww\|=\|\vv\|\,\|\ww\|\,\sin\theta$. ■

Geometry of the cross product

The area of a triangle

• Consider a triangle with two sides $\vv$ and $\ww$
• Think of $\vv$ as the base.
• Length of the base is $b=\|\vv\|$
• Height (at right angles to base) is $h=\|\ww\|\sin \theta$ where $\theta$ is the angle between $\vv$ and $\ww$.
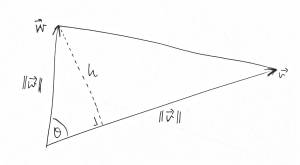
• Hence area of this triangle is $A=\tfrac12 bh=\tfrac12\|\vv\|\,\|\ww\|\sin\theta$
• So $A=\tfrac12\|\vv\times\ww\|$.

The area of a parallelogram

Consider a parallelogram, two of whose sides are $\vv$ and $\ww$.

• area is double the area of the triangle above
• So its area is $A=\|\vv\times\ww\|$.

Example

A triangle with two sides $\vv=\c13{-1}$ and $\ww=\c21{-2}$ has area

• $\tfrac12\|\vv\times\ww\|$
  • $=\tfrac12\left\|\c13{-1}\times\c21{-2}\right\|$
  • $=\tfrac12\left\|\c{-5}0{-5}\right\|=\tfrac52\left\|\c{-1}0{-1}\right\|=\tfrac52\sqrt2$.

The parallelogram with sides $\vv$ and $\ww$ has area

• $\|\vv\times\ww\|=5\sqrt2$.

The volume of a parallelepiped in $\mathbb R^3$

Consider a parallelepiped, with three sides given by $\uu,\vv,\ww$.

• Volume is $V=\left|\det\left[\begin{smallmatrix}u_1&u_2&u_3\\v_1&v_2&v_3\\w_1& w_2&w_3\end{smallmatrix}\right]\right|$

Proof

• Area of base (parallelogram): $A=\|\vv\times\ww\|$
• Volume is $V=Ah$ ($h=$ height, measured at right-angles to the base).
• $\vv\times\ww$ is at right-angles to base
• So $h$ is the length of $\vec p=\text{proj}_{\vv\times\ww}\uu$
• So $ h=\|\text{proj}_{\vv\times\ww}\uu\|=\left\|\frac{\uu\cdot(\vv\times\ww)}{\|\vv\times\ww\|^2}\vv\times\ww\right\| = \frac{|\uu\cdot(\vv\times\ww)|}{\|\vv\times\ww\|}$
• So $V=Ah=|\uu\cdot (\vv\times\ww)| = \left| \det\left[\begin{smallmatrix}u_1&u_2&u_3\\v_1&v_2&v_3\\w_1& w_2&w_3\end{smallmatrix}\right]\right|.$

Example

Find volume of the parallelepiped with vertices including $A=(1,1,1)$, $B=(2,1,3)$, $C=(0,2,2)$ and $D=(3,4,1)$, where $A$ is adjacent to $B$, $C$ and $D$.

Solution

• $\vec{AB}=\c102$, $\vec{AC}=\c{-1}11$ and $\vec{AD}=\c230$ are edges
• Volume is $ V=\left|\det\left[ \begin{smallmatrix}1&0&2\\-1&1&1\\2&3&0\end{smallmatrix}\right] \right| = | 1(0-3)-0+2(-3-2)|$
  • $ = |-13| = 13.$