Last time

• Take a plane $\Pi$ with normal vector $\def\dist{\text{dist}}\def\cp#1#2#3#4#5#6{\left|\begin{smallmatrix}\vec\imath&\vec\jmath&\vec k\\#1&#2&#3\\#4&#5&#6\end{smallmatrix}\right|}\def\nn{\vec n}\def\c#1#2#3{\left[\begin{smallmatrix}#1\\#2\\#3\end{smallmatrix}\right]}\def\uu{\vec u}\def\vv{\vec v}\def\ww{\vec w}\def\bR{\mathbb R}\def\rt{\bR^3}\nn$
• Take a point $A$
• $\dist(A,\Pi)=\frac{|\vec{AB}\cdot \nn|}{\|n\|}$ where $B$ is any point in $\Pi$

The distance from the origin to a plane

• We write $0=(0,0,0)$ for the origin in $\rt$
• Distance from $0$ to a plane $\Pi:ax+by+cz=d$ ?
• Take $B=(d/a,0,0)$ (assuming that $a\ne 0$)
• We get $\dist(0,\Pi)=\frac{|d|}{\|\nn\|}$ where $\nn$ is the normal vector $\nn=\c abc$.
• In particular, if $\nn$ is a unit vector, then $\dist(0,\Pi)=|d|$.
• As $d$ varies (with $\nn$ fixed), we obtain parallel planes at different distances to the origin $0$
• The larger $d$ is, the further the plane is from $0$.

The distance between planes

• Let $\Pi_1$ and $\Pi_2$ be two planes. What is the (shortest) distance between them?
• If they're not parallel, they intersect! So $\dist(\Pi_1,\Pi_2)=0$.
• If they're parallel, then $\dist(\Pi_1,\Pi_2)=\dist(A,\Pi_2)$ for any point $A$ in $\Pi_1$.
  • Why?
  • Since the planes are parallel, $\dist(A,\Pi_2)$ doesn't change if $A$ changes in $\Pi_1$
  • So this is also the shortest distance, for any choice of $A$ in $\Pi_1$

Example

What is the distance between the planes $3x+4y-2z=5$ and $3x+4y-3z=1$?

• The normal vectors are $\c34{-2}$ and $\c34{-3}$
  • They aren't scalar multiples of one another
  • So they're they are in different directions
• So the planes are not parallel.
• So they intersect, and the distance is $0$.

Example

Find the distance between the planes $\Pi_1:3x+4y-2z=5$ and $\Pi_2:3x+4y-2z=1$.

• Same normal vector $\nn=\c34{-2}$, so parallel planes.
• Distance is $\dist(A,\Pi_2)$ where $A$ is any point in $\Pi_1$
  • To find this we also need a point $B$ in $\Pi_2$.
• Choose $A=(1,0,-1)$, $B=(1,0,1)$.
• $\vec {AB}=\c002$ so $\dist(A,\Pi_2) = \frac{|\nn\cdot \vec{AB}|}{\|n\|}=\frac{|0+0+(-2)2|}{\sqrt{3^2+4^2+(-2)^2}} = \frac4{\sqrt{29}}.$

Exercise: a formula for the distance between parallel planes

Show that the distance between the parallel planes $\Pi_1:ax+by+cz=d_1$ and $\Pi_2:ax+by+cz=d_2$ is \[\dist(\Pi_1,\Pi_2)=\frac{|d_2-d_1|}{\|\nn\|},\] where $\nn=\c abc$.

• Important: need equations with the same left hand side.

Example

What is the distance between $x+3y-5z=4$ and $2x+6y-10z=11$?

• Rewrite the second equation as $x+3y-5z=11/2$
• So the planes are parallel, with common normal vector $\nn=\c13{-5}$.
• By the formula, the distance is $\frac{|\tfrac{11}2-4|}{\|\nn\|} = \frac{|\tfrac 32|}{\sqrt{1^2+3^2+(-5)^2}} = \frac3{2\sqrt{35}}$.

Lines in $\mathbb{R}^3$

A line $L$ in $\rt$ has an equation of the form \[ L: \c xyz=\c abc+t\c def, \quad t\in \mathbb R\] where $a,b,c,d,e,f$ are fixed numbers.

• Called a parametric equation
  • because of the variable $t$: a free parameter

• What do $a,b,c,d,e,f$ mean?
  • Set $t=0$: $A=(a,b,c)$ is a point in $L$
  • Set $t=1$: $B=(a+d,b+e,c+f)$ is another
  • So $\vec {AB}=\c def$ is a direction along $L$.

Example

Find the parametric equation of the line $L$ in $\rt$ which passes through $A=(2,1,-3)$ and $B=(4,-1,5)$.

• Note that $\vec{AB}=\c 2{-2}{8}$
• So this is a direction vector along the line $L$
• So the equation is $ L: \c xyz=\c 21{-3}+t\c 2{-2}8,\quad t\in \mathbb{R}$.
• (Same as $ L: \c xyz=\c 4{-1}5+t\c 2{-2}8,\quad t\in \mathbb{R}$).

The distance from a point to a line

How can we find $d=\text{dist}(B,L)$, the distance from the point $B$ to a line $L$?

• Let $A$ be a point on $L$
• Let $\def\vv{\vec v}\vv$ be a direction vector along $L$.
• 
• $\text{dist}(B,L) =\|\vec{AB}\|\,\sin \theta = \frac{\|\vec{AB}\|\,\|\vv\|\sin \theta}{\|\vv\|} = \frac{\|\vec{AB}\times \vv\|}{\|\vv\|}$.

Example

Find the distance from the point $B=(1,2,3)$ to the line \[L:\c xyz=\c10{-1}+t\c41{-5},\quad t\in\mathbb{R}.\]

• Choose $A=\c10{-1}$, in $L$, and $\vv=\c41{-5}$, along $L$
• $\vec{AB}=\c024$, so $ \vec{AB}\times \vv = \cp02441{-5}=\c{-14}{16}{-8}=2\c{-7}{8}{-4}$
• So $\def\dist{\text{dist}}\dist(B,L)=\frac{\|\vec{AB}\times\vv\|}{\|\vv\|}=\frac{2\sqrt{7^2+8^2+4^2}}{\sqrt{4^2+1^2+5^2}} = \frac{2\sqrt{129}}{\sqrt{42}} \approx 3.5051.$

Alternative formula

• $\dist(B,L)=\tfrac{\|\vec{AB}\times \vv\|}{\|\vv\|}$ only works in $\rt$
  • because the cross product is only defined in $\rt$
• 
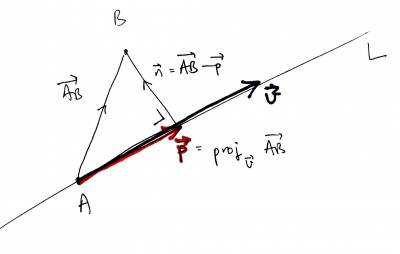
• $\def\pp{\vec p}\dist(B,L)=\|\nn\|=\|\vec{AB}-\pp\|$
  • where $\pp=\def\proj{\text{proj}}\proj_{\vv}\vec{AB}$.
• This works in $\bR^n$ for any $n$

Example

Let's redo the previous example using this method.

We have $\vec{AB}=\c024$ and $\vv=\c41{-5}$, so \[\pp=\proj_{\vv}\vec{AB} = \left(\frac{\vec{AB}\cdot \vv}{\|\vv\|^2}\right)\vv = \frac{0(4)+2(1)+4(-5)}{4^2+1^2+5^2}\c41{-5} = -\frac{18}{42}\c41{-5}=-\frac{3}{7}\c41{-5},\] so \[ \nn=\vec{AB}-\pp=\c024-(-\frac37)\c41{-5}=\c024+\frac37\c41{-5}=\frac17\c{12}{17}{13}\] so \[ \dist(B,L)=\|\nn\|=\frac17\sqrt{12^2+17^2+13^2} = \frac17\sqrt{602} \approx 3.5051.\]

The distance between skew lines in $\mathbb{R}^3$

Suppose that $L_1$ and $L_2$ are skew lines in $\rt$: lines which are not parallel and do not cross.

Let $\vv_1$ be a direction vector along $L_1$, and let $\vv_2$ be a direction vector along $L_2$.

The shortest distance from $L_1$ and $L_2$ is measured along the direction orthogonal to both $\vv_1$ and $\vv_2$, namely the direction of $\nn=\vv_1\times\vv_2$.

Let $\Pi$ be the plane with normal vector $\nn$ which contains $L_1$.

For any point $B$ in $L_2$, we have \[\dist(L_1,L_2)=\dist(B,\Pi) = \frac{|\vec{AB}\cdot \nn|}{\|\nn\|}\] where $A$ is any point in $\Pi$; for example, we can take $A$ to be any point in $L_2$.

To summarise: for skew lines $L_1$ and $L_2$ with direction vectors $\vv_1$ and $\vv_2$, we have \[ \dist(L_1,L_2)=\frac{|\vec{AB}\cdot \nn|}{\|\nn\|}\] where $\nn=\vv_1\times\vv_2$ and $A$ and $B$ are points with one in $L_1$ and the other in $L_2$.

Example

Consider the skew lines \[ L_1:\c xyz=\c 101+t_1\c123,\quad t_1\in\mathbb{R}\] and \[ L_2:\c xyz=\c 321+t_2\c1{-1}1,\quad t_2\in\mathbb{R}.\] The direction vectors are $\c123$ and $\c1{-1}1$, so we take $\nn$ to be their cross product: \[ \nn=\c123\times\c1{-1}1=\begin{vmatrix}\vec\imath&\vec\jmath&\vec k\\1&2&3\\1&-1&1\end{vmatrix}=\c52{-3}\] and if $A=(1,0,1)$ and $B=(3,2,1)$ then $A$ and $B$ are points with one in $L_1$ and the other in $L_2$, and $\vec{AB}=\c 220$. Hence \[\dist(L_1,L_2)=\frac{|\vec{AB}\cdot \nn|}{\|\nn\|}=\frac{2(5)+2(2)+0(-3)}{\sqrt{5^2+2^2+3^2}} = \frac{14}{\sqrt{38}}.\]