Last time
- $\def\bR{\mathbb R}\def\nn{\vec n}\def\i{\vec \imath}\def\j{\vec \jmath}\def\k{\vec k}\def\cp#1#2#3#4#5#6{\left|\begin{smallmatrix}\i&\j&\k\\#1\\#4\end{smallmatrix}\right|}\def\cpc#1#2{\cp{#1_1}{#1_2}{#1_3}{#2_1}{#2_2}{#2_3}}\def\dist{\text{dist}}\dist(X,\Pi)=\frac{|\vec {XY}\cdot \vec n|}{\|\vec n\|}$ is the (shortest) distance from a point $X$ to a plane $\Pi$
- $Y$: any point in $\Pi$
- $\vec n$: a normal vector to $\Pi$
- parametric equation of a line in $\def\rt{\mathbb{R}^3}\rt$:\[L:\quad \def\c#1#2#3{\left[\begin{smallmatrix}#1\\#2\\#3\end{smallmatrix}\right]}\c xyz=\c abc + t\c def,\quad t\in\mathbb R\]with $a,b,c,d,e,f$ constants and $t$ a free parameter
- $(x,y,z)$: typical point in the line $L$
- $(a,b,c)$: one particular point in $L$
- $\c def$: direction vector along $L$
The distance from a point to a line
How can we find $d=\text{dist}(B,L)$, the distance from the point $B$ to a line $L$ in $\mathbb R^3$?
- Let $A$ be a point on $L$
- Let $\def\vv{\vec v}\vv$ be a direction vector along $L$.

- $\text{dist}(B,L) =\|\vec{AB}\|\,\sin \theta = \frac{\|\vec{AB}\|\,\|\vv\|\sin \theta}{\|\vv\|} = \frac{\|\vec{AB}\times \vv\|}{\|\vv\|}$.
Example using $\def\vv{\vec v}\def\dist{\text{dist}}\dist(B,L)=\frac{\|\vec{AB}\times\vv\|}{\|\vv\|}$
Find the distance from the point $B=(1,2,3)$ to the line \[L:\c xyz=\c10{-1}+t\c41{-5},\quad t\in\mathbb{R}.\]
- Choose $A=(1,0,{-1})$, in $L$, and $\vv=\c41{-5}$, along $L$
- $\vec{AB}=\c024$ so $ \vec{AB}\times \vv = \cp02441{-5}=\c{-14}{16}{-8}=2\c{-7}{8}{-4}$
- $\def\dist{\text{dist}}\dist(B,L)=\frac{\|\vec{AB}\times\vv\|}{\|\vv\|}=\frac{2\sqrt{7^2+8^2+4^2}}{\sqrt{4^2+1^2+5^2}} = \frac{2\sqrt{129}}{\sqrt{42}} \approx 3.5051.$
Alternative formula
- $\dist(B,L)=\tfrac{\|\vec{AB}\times \vv\|}{\|\vv\|}$ only works in $\rt$…
- …cross product is only defined in $\rt$!
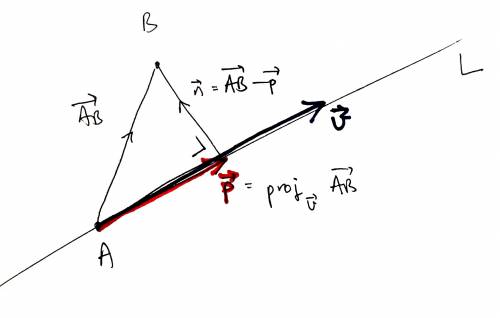
- $\def\pp{\vec p}\dist(B,L)=\|\nn\|=\|\vec{AB}-\pp\|$
- where $\pp=\def\proj{\text{proj}}\proj_{\vv}\vec{AB}$.
- This works in $\bR^n$ for any $n$
Example using $\text{dist}(B,L)=\|\vec{AB}-\vec p\|$
Find the $\dist(B,L)$ for $B=(1,2,3)$ and $L:\c xyz=\c10{-1}+t\c41{-5},\quad t\in\mathbb{R}$.
- $\vec{AB}=\c024$ and $\vv=\c41{-5}$
- $\pp=\proj_{\vv}\vec{AB} = \left(\frac{\vec{AB}\cdot \vv}{\|\vv\|^2}\right)\vv = \frac{-18}{42}\c41{-5}= -\frac{3}{7}\c41{-5}$
- $\nn=\vec{AB}-\pp=\c024-(-\frac37)\c41{-5}=\frac17\c{12}{17}{13}$
- $\dist(B,L)=\|\nn\|=\frac17\sqrt{12^2+17^2+13^2} \approx 3.5051$.
Skew lines in $\mathbb{R}^3$
- Two lines are skew if they are not parallel, and do not cross.
- Skew lines only exist in $\bR^n$ for $n\ge3$.
- Take skew lines $L_1$ and $L_2$ in $\rt$, direction vectors $\vv_1,\vv_2$
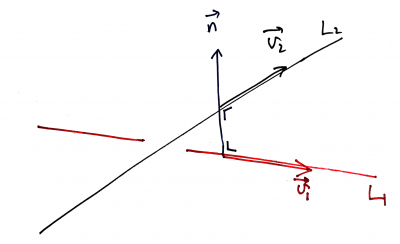
- Let's find a formula for $\dist(L_1,L_2)$
- $\dist(L_1,L_2)$ is measured orthogonal to both $\vv_1$ and $\vv_2$
- i.e. in direction of $\nn=\vv_1\times\vv_2$.
- Let $\Pi$ = plane with normal vector $\nn$ which contains $L_1$.
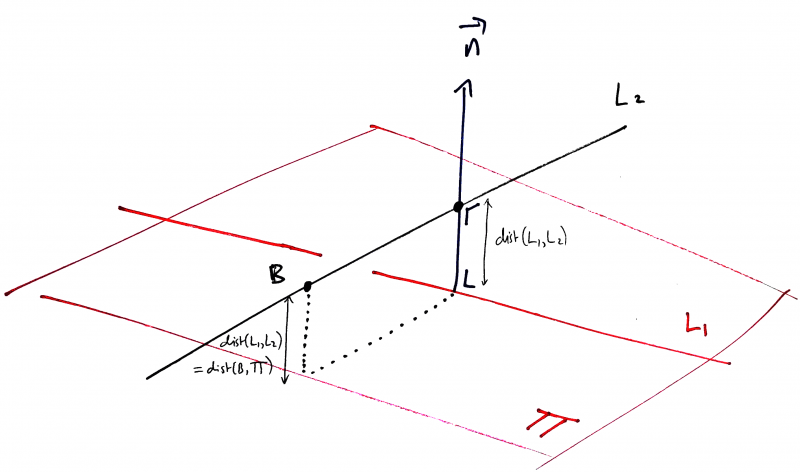
- Let $B$ be in $L_2$, and $A$ in $\Pi$ (e.g. any $A$ in $L_1$)
- Then $\dist(L_1,L_2)=\dist(B,\Pi) = \frac{|\vec{AB}\cdot \nn|}{\|\nn\|}$
Example
What is the distance between the skew lines $L_1:x=1+t_1,\ y=2t_1,\ z=1+3t_1$ and $L_2:\c xyz=\c 321+t_2\c1{-1}1$?
- $\nn=\c123\times\c1{-1}1=\c52{-3}$.
- $A=(1,0,1)$ and $B=(3,2,1)$ are in $L_1$ and $L_2$
- $\vec{AB}=\c 220$
- So $\dist(L_1,L_2)=\frac{|\vec{AB}\cdot \nn|}{\|\nn\|}=\frac{2(5)+2(2)+0(-3)}{\sqrt{5^2+2^2+3^2}} = \frac{14}{\sqrt{38}}$.
Distance between lines in $\mathbb{R}^3$ in general
- The formula $\dist(L_1,L_2)=\frac{|\vec{AB}\cdot \nn|}{\|\nn\|}$ where $\nn=\vec v_1\times \vec v_2$ works for
- skew lines (not parallel, not intersecting)
- actually: any non-parallel lines $L_1$, $L_2$
- What about parallel lines?
- The formula can't work because we'd have $\vec v_1=\vec v_2$ so $\vec n=\vec v_1\times \vec v_2=\vec 0$
- Instead: observe that $\dist(L_1,L_2)=\dist(A,L_2)$ for any point $A$ in $L_1$
- So we can use one of of the point-to-line distance formulae we saw earlier.
End of the course
- Next time: some examples from the most recent exam paper
- Have a look at these before Thursday's lecture to prepare
