Geometry of the cross product

The area of a triangle

• Consider a triangle with two sides $\def\c#1#2#3{\left[\begin{smallmatrix}#1\\#2\\#3\end{smallmatrix}\right]}\def\uu{\vec u}\def\vv{\vec v}\def\ww{\vec w}\def\bR{\mathbb R}\vv$ and $\ww$
• Think of $\vv$ as the base.
• Length of the base is $b=\|\vv\|$
• Height (at right angles to base) is $h=\|\ww\|\sin \theta$ where $\theta$ is the angle between $\vv$ and $\ww$.
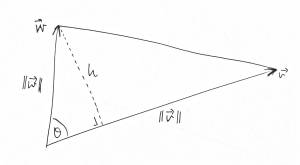
• Hence area of this triangle is $A=\tfrac12 bh=\tfrac12\|\vv\|\,\|\ww\|\sin\theta$
• So $A=\tfrac12\|\vv\times\ww\|$.

The area of a parallelogram

Consider a parallelogram, two of whose sides are $\vv$ and $\ww$.

• area is double the area of the triangle above
• So its area is $A=\|\vv\times\ww\|$.

Example

A triangle with two sides $\vv=\c13{-1}$ and $\ww=\c21{-2}$ has area

• $\tfrac12\|\vv\times\ww\|$
  • $=\tfrac12\left\|\c13{-1}\times\c21{-2}\right\|$
  • $=\tfrac12\left\|\c{-5}0{-5}\right\|=\tfrac52\left\|\c{-1}0{-1}\right\|=\tfrac52\sqrt2$.

The parallelogram with sides $\vv$ and $\ww$ has area

• $\|\vv\times\ww\|=5\sqrt2$.

The volume of a parallelepiped in $\mathbb R^3$

Consider a parallelepiped, with three sides given by $\uu,\vv,\ww$.

• Volume is $V=\left|\det\left[\begin{smallmatrix}u_1&u_2&u_3\\v_1&v_2&v_3\\w_1& w_2&w_3\end{smallmatrix}\right]\right|$

Proof

• Area of base (parallelogram): $A=\|\vv\times\ww\|$
• Volume is $V=Ah$ ($h=$ height, measured at right-angles to the base).
• $\vv\times\ww$ is at right-angles to base
• So $h$ is the length of $\vec p=\text{proj}_{\vv\times\ww}\uu$
• So $ h=\|\text{proj}_{\vv\times\ww}\uu\|=\left\|\frac{\uu\cdot(\vv\times\ww)}{\|\vv\times\ww\|^2}\vv\times\ww\right\| = \frac{|\uu\cdot(\vv\times\ww)|}{\|\vv\times\ww\|}$
• So $V=Ah=|\uu\cdot (\vv\times\ww)| = \left| \det\left[\begin{smallmatrix}u_1&u_2&u_3\\v_1&v_2&v_3\\w_1& w_2&w_3\end{smallmatrix}\right]\right|.$

Example

Find volume of the parallelepiped with vertices including $A=(1,1,1)$, $B=(2,1,3)$, $C=(0,2,2)$ and $D=(3,4,1)$, where $A$ is adjacent to $B$, $C$ and $D$.

Solution

• $\vec{AB}=\c102$, $\vec{AC}=\c{-1}11$ and $\vec{AD}=\c230$ are edges
• Volume is $ V=\left|\det\left[ \begin{smallmatrix}1&0&2\\-1&1&1\\2&3&0\end{smallmatrix}\right] \right| = | 1(0-3)-0+2(-3-2)|$
  • $ = |-13| = 13.$

Planes and lines in $\mathbb{R}^3$

Planes in $\mathbb{R}^3$

• Typical plane in $\bR^3$ has equation $ ax+by+cz=d$
  • $a,b,c,d$ are constants
• Same as $\def\nn{\vec n}\nn\cdot \c xyz=d$ where $\def\nn{\vec n}\nn=\c abc$

Normal vectors to a plane

• Consider a plane $\Pi$ given by $\nn\cdot \c xyz=d$
• Take $A=\def\cc#1{(x_{#1},y_{#1},z_{#1})}\cc1$, $B=\cc2$ in $\Pi$
• Say vector $\vec{AB}$ is in $\Pi$ or parallel to $\Pi$
• $ \vec n\cdot \vec{AB}=\nn\cdot\def\cp#1{\c{x_{#1}}{y_{#1}}{z_{#1}}}\left(\cp2-\cp1\right)$
  • $ = \nn\cdot\cp2-\nn\cdot\cp1=d-d=0$
• So $\nn\cdot\vv=0$ for every vector $\vv$ in $\Pi$.
• So $\nn$ is orthogonal to every vector in $\Pi$.
• We call $\nn$ a normal vector to $\Pi$.

Normal vectors to a plane

Example

Find a unit normal vector to the plane $x+y-3z=4$.

Solution

• $\nn=\c11{-3}$ is a normal vector to this plane
• So $\vv=\frac1{\|\nn\|}\nn=\frac1{\sqrt{11}}\c11{-3}$ is a unit normal vector to this plane.

Example 2

Find the equation of the plane with normal vector $\c1{-3}2$ which contains the point $(1,-2,1)$, and find three other points in the plane.

Solution

• Equation is $x-3y+2z=d$ for some $d$
• Find $d$ by subbing in $(x,y,z)=(1,-2,1)$
  • $1-3(-2)+2(1)=d$, so $d=9$
• Equation $x-3y+2z=9$.
• By inspection, some other points in this plane are $(9,0,0)$, $(0,1,6)$, $(1,1,\tfrac{11}2)$

Example 3

What's the equation of the plane parallel to $\c111$ and $\c1{-1}1$ containing the point $(3,0,1)$?

• A normal vector is $\nn=\c111\times\c1{-1}1=\def\cp#1#2#3#4#5#6{\left|\begin{smallmatrix}\vec\imath&\vec\jmath&\vec k\\#1&#2&#3\\#4&#5&#6\end{smallmatrix}\right|}\cp1111{-1}1=\c{2}0{-2}$
• So the equation is $2x+0y-2z=2(3)-2(1)=4$,
• or $2x-2z=4$
• or $x-z=2$.

Example 4

Find the equation of the plane $\Pi$ containing $A=(1,2,0)$, $B=(3,0,1)$ and $C=(4,3,-2)$.

Solution

• $\vec{AB}=\c2{-2}1$ and $\vec{AC}=\c31{-2}$ are both vectors in $\Pi$
• Need $\nn$, orthogonal to both. Use cross product!
• $\nn=\vec{AB}\times\vec{AC}=\cp2{-2}131{-2}=\c378$
• Equation is $3x+7y+8z=d$; find $d=17$ by subbing in $A=(1,2,0)$
• Answer: $ 3x+7y+8z=17$.

Parallel planes

Let $\Pi_1$ be a plane with normal vector $\nn_1$, and let $\Pi_2$ be a plane with normal vector $\nn_2$.

• $\Pi_1$ and $\Pi_2$ are parallel planes if $\nn_1$ and $\nn_2$ are are in the same direction
  • If $\Pi_1$ has equation $ax+by+cz=d_1$ then any parallel plane $\Pi_2$ has an equation which may be written with the same left hand side: $ax+by+cz=d_2$.
  • i.e., we can assume that $\nn_1=\nn_2=\c abc$.

Example

The plane parallel to $2x-4y+5z=8$ passing through $(1,2,3)$ is

• $2x-4y+5z=2(1)-4(2)+5(3) = 10$
• i.e., $2x-4y+5z=10$.

Orthogonal planes

Let~$\Pi_1$ be a plane with normal vector $\nn_1$ and let $\Pi_2$ be a plane with normal vector $\nn_2$.

$\Pi_1$ and $\Pi_2$ are orthogonal or perpendicular planes if they meet at right angles. The following conditions are equivalent:

1. $\Pi_1$ and $\Pi_2$ are orthogonal planes;
2. $\nn_1\cdot\nn_2=0$;
3. $\nn_1$ is a vector in $\Pi_2$;
4. $\nn_2$ is a vector in $\Pi_1$.

Example 1

Find the equation of the plane $\Pi$ passing through $A=(1,3,-3)$ and $B=(4,-2,1)$ which is orthogonal to the plane $x-y+z=5$.

• $x-y+z=5$ has normal $\c1{-1}1$; this is in $\Pi$.
• $\vec{AB}=\def\c#1#2#3{\left[\begin{smallmatrix}#1\\#2\\#3\end{smallmatrix}\right]}\c3{-5}4$ is also a vector in $\Pi$
• Normal for $\Pi$: $\def\nn{\vec n}\nn=\c1{-1}1\times\c3{-5}4=\cp1{-1}13{-5}4=\c1{-1}{-2}$.
• Sub in $A$ (or $B$): get $x-y-2z=4$.

Example 2

Find the equation of the plane $\Pi$ which contains the line of intersection of the planes \[ \Pi_1: x-y+2z=1\quad\text{and}\quad \Pi_2: 3x+2y-z=4,\] and is perpendicular to the plane $\Pi_3:2x+y+z=3$.

• First find the line of intersection of $\Pi_1$ and $\Pi_2$
• Solve $x-y+2z=1$, $3x+2y-z=4$
• $\left[\begin{smallmatrix}1&-1&2&1\\3&2&-1&4\end{smallmatrix}\right]\to_{EROs}\left[\begin{smallmatrix}1&0&3/5&6/5\\0&1&-7/5&1/5\end{smallmatrix}\right]$
• Line $L$ of intersection is $\c xyz=\c{6/5}{1/5}0+t\c{-3/5}{7/5}1$, $t\in\mathbb{R}$.

• $\Pi$ contains $L:\c xyz=\c{6/5}{1/5}0+t\c{-3/5}{7/5}1$, $t\in\mathbb{R}$, orthogonal to $\Pi_3: 2x+y+z=3$
• $5\c{-3/5}{7/5}1=\c{-3}75$ is a vector along $L$, so in $\Pi$
• $\Pi_3$ has normal vector $\nn_3=\c211$, which is in $\Pi$.
• Normal vector for $\Pi$: $\nn=\c211\times\c{-3}75 = \cp211{-3}75=\c{-2}{-13}{17}$
• $\Pi$ has equation $-2x-13y+17z=d$

• $\Pi$ has equation $-2x-13y+17z=d$ and contains $L:\c xyz=\c{6/5}{1/5}0+t\c{-3/5}{7/5}1$, $t\in\mathbb{R}$
• Take $t=2$: $(0,3,2)$ in $L$, so in $\Pi$
• Sub in: $d=0-13(3)+17(2)=-39+34=-5$
• Answer: $-2x-13y+17z=-5$, or $2x+13y-17z=5$.