↓ Slide 1

Last time

the vector $\vec{AB}$ joining $A$ to $B$
length (norm) of a vector
unit vectors
triangle law and parallelogram law for vector addition

→ Slide 2

The dot product

↓ Slide 3

Definition of the dot product

Let $\def\m#1{\left[\begin{smallmatrix}#1\end{smallmatrix}\right]}\vec v=\m{v_1\\v_2\\\vdots\\v_n}$ and $\vec w=\m{w_1\\w_2\\\vdots\\w_n}$ be two vectors in $\mathbb{R}^n$.

The dot product of $\vec v$ and $\vec w$ is the number $\vec v\cdot \vec w$ given by \[ \color{red}{\vec v\cdot\vec w=v_1w_1+v_2w_2+\dots+v_nw_n}.\]

In other words, $\vec v\cdot \vec w$ is the row-column product $(\vec v)^T\vec w$ of the transpose of $\vec v$ with $\vec w$.
Note that while $\vec v$ and $\vec w$ are vectors, their dot product $\vec v\cdot \vec w$ is a scalar.

↓ Slide 4

Example

Let $\vec v=\m{3\\5}$ and $\vec w=\m{4\\-7}$.

$\vec v\cdot \vec w=\m{3\\5}\cdot \m{4\\-7} = 3(4)+5(-7)=12-35=-23$.

→ Slide 5

Properties of the dot product

For any vectors $\vec v$, $\vec w$ and $\vec u$ in $\mathbb{R}^n$, and any scalar $c\in \mathbb{R}$:

$\def\dp#1#2{\vec #1\cdot \vec #2}\dp vw=\dp wv$ (the dot product is commutative)
$\vec u\cdot(\vec v+\vec w)=\dp uv+\dp uw$
$(c\vec v)\cdot \vec w=c(\dp vw)$
$\dp vv=\|\vec v\|^2\ge 0$, and $\dp vv=0 \iff \vec v=0_{n\times 1}$

The proofs of these properties are exercises.

→ Slide 6

Angles and the dot product

↓ Slide 7

Theorem: geometric dot product formula

If $\vec v$ and $\vec w$ are non-zero vectors in $\mathbb{R}^n$, then \[ \dp vw=\|\vec v\|\,\|\vec w\|\,\cos\theta\] where $\theta$ is the angle between $\vec v$ and $\vec w$.

Why's it called a geometric formula?
- It expresses the dot product using only geometric quantities: lengths and angle
The proof will be given soon, but for now let's work out an example.

↓ Slide 8

Example

What's the angle $\theta$ between $\vec v=\m{1\\2}$ and $\vec w=\m{-2\\1}$?

$\|\vec v\|\,\|\vec w\|\cos\theta=\dp vw$
$=1(-2)+2(1)=-2+2=0$.
So $\|\vec v\|\,\|\vec w\|\cos\theta=0$
We have $\|\vec v\|\,\|\vec w\|\ne 0$ (why?) so we can cancel this from both sides
So $\cos\theta=0$
So $\theta=\pi/2$ or $\theta=3\pi/2$ (measuring angles in radians).
The angle between $\vec v$ and $\vec w$ is a right angle.
We say $\vec v$ and $\vec w$ are orthogonal.

↓ Slide 9

Picture of $\vec v=\m{1\\2}$ and $\vec w=\m{-2\\1}$

We can draw a convincing picture which indicates that these vectors are indeed at right angles:

↓ Slide 10

Reminder: the cosine rule

This is the key to proving the geometric dot product formula.

↓ Slide 11

Proof of the geometric dot product formula

Aim: $\def\vv{\vec v}\def\ww{\vec w}\vv\cdot\ww=\|\vv\|\,\|\ww\|\cos\theta$.

Consider a triangle with two sides $\vv$ and $\ww$. By the triangle rule for vector addition, the third side is $\vv-\ww$:
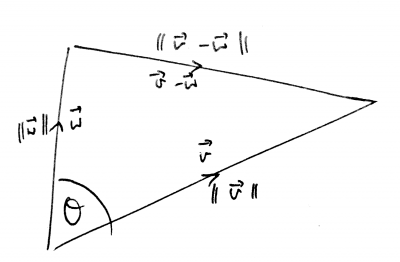
Use the cosine rule with $A=\theta$, $a=\|\vv-\ww\|$, $b=\|\vv\|$, $c=\|\ww\|$
$ \|\vv-\ww\|^2=\|\vv\|^2+\|\ww\|^2-2\|\vv\|\,\|\ww\|\,\cos\theta$

↓ Slide 12

Proof of the geometric dot product formula, continued

Aim: $\def\vv{\vec v} \def\ww{\vec w}\vv\cdot\ww=\|\vv\|\,\|\ww\|\cos\theta$.

$\|\vv-\ww\|^2=\|\vv\|^2+\|\ww\|^2-2\|\vv\|\,\|\ww\|\,\cos\theta$
So $2\|\vv\|\,\|\ww\|\cos\theta=\|\vv\|^2+\|\ww\|^2-\|\vv-\ww\|^2$
- $=\vv\cdot\vv+\ww\cdot\ww-(\vv-\ww)\cdot(\vv-\ww)$
- $=\vv\cdot\vv+\ww\cdot\ww-(\vv\cdot\vv+\ww\cdot\ww-\ww\cdot\vv-\vv\cdot\ww)$
- $=2\vv\cdot\ww$.
So $2\vv\cdot\ww=2\|\vv\|\,\|\ww\|\,\cos\theta$
So $\vv\cdot\ww=\|\vv\|\,\|\ww\|\cos\theta$. ■

↓ Slide 13

Corollary 1: angle formula

If $\vv$ and $\ww$ are non-zero vectors and $\theta$ is the angle between them, then $\cos\theta=\displaystyle\frac{\vv\cdot\ww}{\|\vv\|\,\|\ww\|}$.

Proof: since $\vv$ and $\ww$ are non-zero, we have $\|\vv\|\,\|\ww\|\ne0$ so we can divide both sides of the geometric dot product formula by $\|\vv\|\,\|\ww\|$ to get the angle formula.

↓ Slide 14

Example 1

What is the angle $\theta$ between $\def\c#1#2{\left[\begin{smallmatrix}{#1}\\{#2}\end{smallmatrix}\right]}\c12$ and $\c3{-4}$?

Use the angle formula $\cos\theta=\frac{\vv\cdot\ww}{\|\vv\|\,\|\ww\|}$:
$ \cos\theta=\frac{\c12\cdot\c3{-4}}{\left\|\c12\right\|\,\left\|\c3{-4}\right\|} =\frac{3-8}{\sqrt5\sqrt{25}}=\frac{-5}{5\sqrt 5}=-\frac1{\sqrt5}$
So $\theta=\cos^{-1}(-\tfrac1{\sqrt5}) \approx 2.03\,\text{radians}\approx 116.57^\circ$.

↓ Slide 15

Corollary 2: orthogonal vectors

If $\vv$ and $\ww$ are non-zero vectors with $\vv\cdot\ww=0$, then $\vv$ and $\ww$ are orthogonal: they are at right-angles.

Proof: the angle formula gives $\cos \theta=\frac{\vv\cdot\ww}{\|\vv\|\,\|\ww\|}=0$
So $\cos\theta=0$
So $\theta$ is a right-angle.

↓ Slide 16

Example 2

Prove that $A=(2,3)$, $B=(3,6)$ and $C=(-4,5)$ are the vertices of a right-angled triangle.

$\vec{AB}=\c36-\c23=\c13$
$\vec{AC}=\c{-4}5-\c23=\c{-6}2$
So $\vec{AB}\cdot\vec{AC}=\c13\cdot\c{-6}2=1(-6)+3(2)=0$
So the sides $AB$ and $AC$ are at right-angles.
So $ABC$ is a right-angled triangle.

↓ Slide 17

Example 3

Find a unit vector orthogonal to the vector $\vv=\c12$.

Observe that $\ww=\c{-2}1$ has $\vv\cdot\ww=0$
So $\vv$ and $\ww$ are orthogonal
$\vec u=\frac1{\|\ww\|}\ww$ is a unit vector in the same direction as $\ww$
- so it is also orthogonal to $\vv$.
So $\vec u=\frac1{\sqrt5}\c{-2}1=\c{-2/\sqrt5}{1/\sqrt5}$ is a unit vector orthogonal to $\vv=\c12$.