Chapter 1: Systems of linear equations

Linear equations

First example: a linear equation in two variables

Consider the equation \[ 2x+5y=7.\] This is an equation in two variables, or indeterminates, $x$ and $y$.

A solution of this equation is a pair of numbers $(a,b)\in \mathbb{R}^2$ so that if we replace $x$ with $a$ and replace $y$ with $b$, then the equation becomes true.

In other words, so that $2a+5b$ really is equal to $7$.

• $(3,1)$ is not a solution, because $2\times 3+5\times 1\ne 7$
• $(1,1)$ is a solution, because $2\times 1+5\times 1=7$
• Other solutions include $(0,\tfrac 75)$, $(0.5,1.2)$, $(6,-1)$, $(3.5,0)$, $(-\tfrac32,2)$, …

We can't make a complete list of all solutions, since there are infinitely many solutions in $\mathbb{R}^2$. However, we can draw the set of all solutions as a subset of $\mathbb{R}^2$. This turns out to be a straight line:

We say that the equation $2x+5y=7$ is a linear equation in two variables.

Definition

More examples of linear equations in two variables

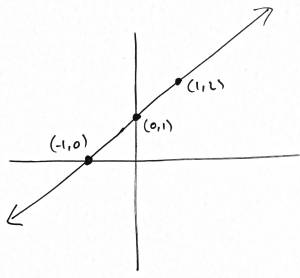
• $y-x=1$
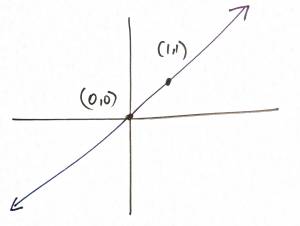
• $x-y=0$
• $x=0\iff 1x+0y=0$