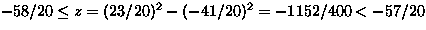UCD Openday 1998
Mathematics Problem
You must follow the rules.
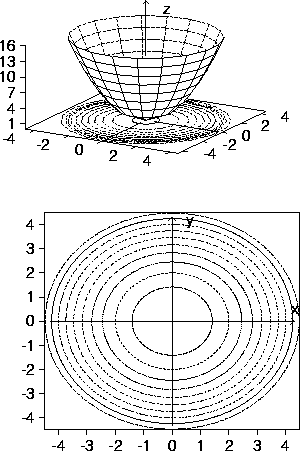
(i) parabolic bowl, graph of
z=f(x,y)=x2+y2
and
(ii) contour diagram of z=f(x,y)=x2+y2
A function of the form z=f(x,y) generates a contour diagram
consisting of fixed height curves of f.
The example above shows the contour diagram lying under
the graph z=f(x,y)= x2 + y2.
An apparently sensible rule to digitize such a diagram
(i.e., to transform it into a tiled pattern) fails
spectacularly, but generates an interesting black and white grid.
The actual question follows.
Tiled Contour Problem
Create a contour diagram of the function
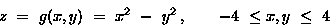
by drawing (a representative selection of) the curves
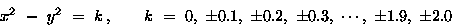
Plan
to create the above contour diagram on the square
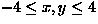 : use 160x160=25600 square tiles,
each with side of length 1/20 and each either
black or white. To decide the colour of any tile:-
: use 160x160=25600 square tiles,
each with side of length 1/20 and each either
black or white. To decide the colour of any tile:-
-
find (x,y) the coordinates of its lower left corner
-
round g(x,y) down to
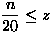 , the nearest integer multiple
of 1/20 not greater than z
, the nearest integer multiple
of 1/20 not greater than z
-
if n is an even integer use a black tile; this tile
is considered to lie on one of the contours, see above
-
if n is odd use a white tile; this
tile is considered to lie between the contours, see above
For example: the tile with lower left corner
at (x,y)=(23/20,-47/20) is white because
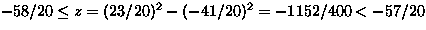
thus n=-58 which is even.
Describe the resulting tile pattern, which is very
different from what was expected.
Explain how this pattern might have been anticipated.
Page maintained by
jbquig@ucd.ie
Revised 23 Mar 1998.


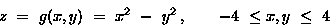
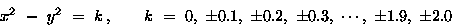
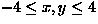 : use 160x160=25600 square tiles,
each with side of length 1/20 and each either
black or white. To decide the colour of any tile:-
: use 160x160=25600 square tiles,
each with side of length 1/20 and each either
black or white. To decide the colour of any tile:-
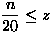 , the nearest integer multiple
of 1/20 not greater than z
, the nearest integer multiple
of 1/20 not greater than z